12

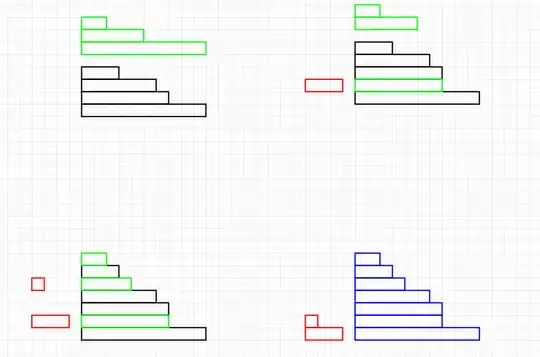
Define the $q$-binomial (Gaussian) coefficient ${n+m\brack n}_q$ as the generating function for integer partitions (whose Ferrers diagrams are) fitting into a rectangle $n\times m$, i.e., for the set $P_{n,m}$ of partitions with at most $n$ parts, all at most $m$. From this definition, the $q$-analogs of Pascal's triangle identities, such as ${n+m\brack n}_q={n+m-1\brack n-1}_q+q^n{n+m-1\brack n}_q$, have straightforward combinatorial proofs which are also reminiscent of the ones for classical binomial coefficients (consider on one side the partitions which fit into the smaller rectangle $(n-1)\times m$, and on the other side those which do not, ergo fit in the rectangle $n\times(m-1)$ once one has removed their first column, with size $n$).

Now, the exact formula $${n+m\brack n}_q=\frac{(q)_{n+m}}{(q)_n\,(q)_m},$$ where $(q)_n:=(1-q)(1-q^2)\cdots(1-q^n)$, may then be proved by induction. However, one may rewrite this formula as $${n+m\brack n}_q\times\frac1{(q)_{n+m}}=\frac1{(q)_n}\times\frac1{(q)_m}.$$ Recalling that $\frac1{(q)_n}$ is the generating function for the set $P_n$ of partitions into at most $n$ parts (likewise, by conjugation, for the set $P'_n$ of partitions into parts at most $n$), this suggests that the sets $P_{n,m}\times P_{n+m}$ and $P_n\times P'_m$ are in bijection, where obviously $P_{n,m}=P_n\cap P'_m$.

My question is whether a simple bijection exists. Say, given a pair $(\lambda,\mu)\in P_n\times P'_m$ of Ferrers diagrams which respectively fit into the rectangles $n\times\infty$ and $\infty\times m$, can we construct two other diagrams $(\nu,\eta)\in P_{n,m}\times P_{n+m}$ which respectively fit into the rectangles $n\times m$ and $(n+m)\times\infty$, in such a way that the map $(\lambda,\mu)\mapsto(\nu,\eta)$ is one-to-one?

Intuitively, any "merging" of $\lambda$ and $\mu$ (or its conjugate $\mu'$) produces an element $\eta\in P_{n+m}$. Of course, since many pairs $(\lambda,\mu)$ would yield the same $\eta$, one needs to "store" as much information as possible about $(\lambda,\mu)$ into the partition $\nu$ to make the merging one-to-one. What puzzles me is that only a rectangle $n\times m$ of information seems enough.

Jyrki Lahtonen
  • 140,891
nejimban
  • 4,107
  • I think this is already an interesting question if it's restricted to the case $m=1$, looking for a bijection between $[0, n] \times P_{n+1}$ and $P_n \times \mathbb{N}_0$. – Peter Taylor May 16 '18 at 16:03
  • 1
    It's not too hard to intuit that there's enough information if you interpret $\nu$ as a lattice walk from $(0, 0)$ to $(n, m)$ using steps $(1, 0)$ and $(0, 1)$: then there is a standard combinatorial interpretation of the $\binom{n+m}{n}$ elements of $P_{n,m}$ as selecting which of the $n+m$ steps are $(1, 0)$. But selecting $n$ of $n+m$ elements is clearly sufficient to separate out the $n+m$ parts of $\eta$ into the $n$ parts of $\lambda$ and the $m$ parts of $\mu$. – Peter Taylor May 17 '18 at 14:54
  • The hard part, in fact, is to explain why $\nu$ doesn't give too much information, in the sense that when $\lambda$ and $\mu$ have some parts in common, those parts become indistinguishable when mixed in $\eta$, so that the separation process sketched in the previous comment is surjective but not injective. – Peter Taylor May 17 '18 at 14:55
  • I think that if you can prove the "upper decrementation identity" $\displaystyle \dfrac{1}{1-q^a} {a \brack b}_q = \dfrac{1}{1-q^{a-b}} {a-1 \brack b}_q$ (for $a > b \geq 0$) bijectively, then you can get your identity by applying it multiple times (each time decrementing the numerator of $\displaystyle {n+m \brack n}_q$). Of course, this will yield a recursive bijection, but that shouldn't be particularly unheard in partition theory :) – darij grinberg May 17 '18 at 23:52
  • I think I see how to bijectively prove the "upper decrementation identity" (though I am not 100% sure). Say that a partition $\lambda$ is stylite all its parts are $\leq a-b$ and if it has at most $b$ parts smaller than $a-b$ (but may have any number of parts equal to $a-b$). I claim that the size-generating function of all stylite partitions equals both sides of the identity. For the right hand side, this is obvious: The factor $\dfrac{1}{1-q^{a-b}}$ counts the arbitrarily many parts equal to $a-b$ that the partition may have, while the ... – darij grinberg May 18 '18 at 10:16
  • ... factor $\displaystyle {a-1 \brack b}_q$ counts the remaining parts. For the left hand side, I claim that a partition $\lambda$ is stylite if and only if its $a$-core fits into the $b \times \left(a-b\right)$-rectangle and its $a$-quotient -- not sure about this anymore. – darij grinberg May 18 '18 at 10:21

1 Answers1

10

We begin by describing a process to merge two partitions. Let $P_n$ be a partition into at most $n$ parts and $\color{green}{P_m}$ into at most $\color{green}{m}$ parts. Now take the largest part/row of the second partition and let it "sink" into the first partition; more formally, while it is longer than a part in the first partition place it at at a lower level BUT each time it moves past a row remove one square (& record this by placing a red square to left). Continue this process with each of the next largest part until all of the parts have been merged.

This process is illustrated in the diagram below for the partitions $\color{green}{10+5+2}$ and $10+7+6+3$ & they merge to create the partition $\color{blue}{10+7+7+6+4+3+2}$. Now collect all the red parts together in the order that they were formed, they will form a partition whose parts are of size at most $n$ and with $m$ parts; i.e an element of $\color{red}{{n+m\brack n,m}_q}$. (The partition formed in this case is $\color{red}{3+1+0}$.)

enter image description here

This process is easily reversed. (I should probably justify this claim ?)

It is reasonably easy to see that this give the required bijection \begin{eqnarray*} \color{red}{{n+m\brack n,m}_q}\times\color{blue}{\frac1{(q)_{n+m}}}=\frac1{(q)_n}\times\color{green}{\frac1{(q)_m}}. \end{eqnarray*}

Donald Splutterwit
  • 37,323
  • Great answer. Indeed, if one sees the partition $\nu$ fitting in the $m\times n$ rectangle (the $\color{red}{\text{red}}$ partition in your diagram) as "a partition with exactly $m$ parts all at most $n$, but with possibly zero parts", then your step-by-step procedure is easily reversed. – nejimban May 21 '18 at 10:51
  • In fact this gives more than the required bijection, in the expected way: since the generating function identity implies an identity of each coefficient of $q^k$, we might expect that the bijection would map $(\lambda, \mu)$ to $(\nu, \eta)$ in such a way that $|\lambda| +|\mu| = |\nu| + |\eta|$, and this does just that. – Peter Taylor May 21 '18 at 11:31