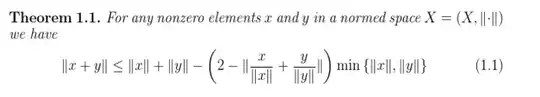First, take $(a, b) = \left( \dfrac{1}{2}, -\dfrac{1}{2} \right)$, then $λ \geqslant 2^{p - 2}$. Now it will be proved that for $λ = 2^{p - 2}$, the inequality holds. Note that $f(x) = \dfrac{x^p}{1 - x}$ is increasing on $[0, 1)$. If $ab \geqslant 0$, without loss of generality, suppose $a \geqslant b \geqslant 0$, then$$
(1) \Longleftrightarrow \frac{(a - b)^p}{2 - (a - b)} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} - \frac{b^p}{1 - b} \right).
$$
If $ab < 0$, without loss of generality, suppose $a > 0 > b$, then$$
(1) \Longleftrightarrow \frac{(a + (-b))^p}{2 - (a + (-b))} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} + \frac{(-b)^p}{1 - (-b)} \right).
$$
Thus it suffices to prove that for any $0 \leqslant b \leqslant a < 1$,$$
\frac{(a - b)^p}{2 - (a - b)} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} - \frac{b^p}{1 - b} \right),\\
\frac{(a + b)^p}{2 - (a + b)} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} + \frac{b^p}{1 - b} \right).
$$
Note that$$
f''(x) = (p - 1)p · \frac{x^{p - 2}}{1 - x} + 2p · \frac{x^{p - 1}}{(1 - x)^2} + 2 · \frac{x^p}{(1 - x)^3}, \quad \forall 0 < x < 1
$$
thus $f$ is convex on $[0, 1)$. By Jensen's inequality,$$
\frac{1}{2} \left( \frac{a^p}{1 - a} + \frac{b^p}{1 - b} \right) \geqslant \frac{\left( \dfrac{a + b}{2} \right)^p}{1 - \dfrac{a + b}{2}},
$$
i.e.$$
\frac{(a + b)^p}{2 - (a + b)} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} + \frac{b^p}{1 - b} \right).
$$
Now for any fixed $0 \leqslant c < 1$, define$$
g_c(x) = f(x + c) - f(x) = \frac{(x + c)^p}{1 - (x + c)} - \frac{x^p}{1 - x}. \quad 0 \leqslant x < 1 - c
$$
Because $f''(x) \geqslant 0$ implies $f'$ is increasing on $[0, 1)$, then $g_c'(x) = f'(x + c) - f'(x) \geqslant 0$, and $g_c'$ is increasing on $[0, 1 - c)$. Thus$$
\frac{a^p}{1 - a} - \frac{b^p}{1 - b} = g_{a - b}(b) \geqslant g_{a - b}(0) = \frac{(a - b)^p}{1 - (a - b)}.
$$
Since$$
2^{p - 2} \frac{(a - b)^p}{1 - (a - b)} \geqslant \frac{(a - b)^p}{2 - (a - b)} \Longleftrightarrow \frac{1 - (a - b)}{2 - (a - b)} \leqslant 2^{p - 2},
$$
and $0 \leqslant a - b < 1$ implies $\dfrac{1 - (a - b)}{2 - (a - b)} \leqslant \dfrac{1}{2} < 2^{p - 2}$, then$$
\frac{(a - b)^p}{2 - (a - b)} \leqslant 2^{p - 2} \left( \frac{a^p}{1 - a} - \frac{b^p}{1 - b} \right).
$$
Therefore,$$
|a - b|^p \leqslant 2^{p - 2} (2 - |a - b|) \left| \frac{a |a|^{p - 1}}{1 - |a|} - \frac{b |b|^{p - 1}}{1 - |b|} \right|. \quad \forall a, b \in (-1, 1)
$$