Let $P = \{(x,y) \in \mathbb R^2 : x^2+y^2<1 \}$ and $Q = \{(1,x) : x \in \mathbb R\}$. Is $X=P \cup Q$ connected?

Question

If I look just at $P$, I conclude $P$ is connected. $Q$ is a vertical line and is also connected. How to see their union is connected or not?

I can see that $X=P \cup Q$ is pathwise connected (geometrically) if I can join any two points of $X$ by a path (line) which lies inside this set, does pathwise connectedness implies connectedness?

For some basic information about writing math at this site see e.g. basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. — GNUSupporter 8964民主女神地下教會, Apr 06 '18 at 20:07

GNUSupporter 8964民主女神地下教會 · Accepted Answer · 2018-04-07T14:15:39.027

3

Observe that $P$ (unit open disc) and $Q$ (vertical line touching $P$ at $(1,0)$) are both convex, so path-connected.

It's clear that the segment $S = [\frac12, 1] \times \{0\}$ is contained in $P \cup Q$.

$[\frac12, 1) \times \{0\} \subseteq P$
$(1,0) \in Q$

The segment $S$ is path connected, and both path connected $P$ and $Q$ have nonempty intersection with $S$, so $P \cup S \cup Q = P \cup Q$ is path connected.

(Edited in response to MikeMathMan's comment)

To show the path connectedness implies connectedness, we use a classic proof by contradiction. Let $X$ be a path-connected space and $U$, $V$ be two open sets that separate $X$. (i.e. $U \sqcup V = X$, where $\sqcup$ denotes disjoint union.) $\gamma: [0,1] \to X$ be a continuous path starting at $u \in U$ and ending at $v \in V$. (i.e. $\gamma(0) = u$, $\gamma(1) = v$) Due to the continuity of $\gamma$, $\gamma^{-1}(U)$ and $\gamma^{-1}(V)$ are both nonempty and open in $[0,1]$, but they separate $[0,1]$, contradiction.

edited Apr 07 '18 at 14:15

answered Apr 06 '18 at 20:19

GNUSupporter 8964民主女神地下教會

17,998

Thank you , you apply this theorem ? - Union of P and Q are connected if they have non empty intesections provided P and Q are connected , so you constructed one more connected set S so that S,P,Q are connected and S intersection P intersection Q is non empty am i right ?? – user534210 Apr 06 '18 at 20:34
@user534210 Yes, it's an intuitive result "the union of a collection of connected subspaces of $X$ that have a point in common is connected" (Thm 23.3 in Munkres' Topology.) I've [edit]ed my answer to give a stronger and more intuitive (in the visual sense) result. – GNUSupporter 8964民主女神地下教會 Apr 06 '18 at 20:43
1

Thank you very much .... – user534210 Apr 06 '18 at 20:49
@user534210 I've added a picture to give an illustration. If "connectedness" is replaced by "path connectedness" in the quoted theorem, then it's much easier to see. – GNUSupporter 8964民主女神地下教會 Apr 06 '18 at 20:53
i have one more problem of james mukre 's , topologists sine curve is connected but not pathwise connected , can you explain me , i will post a question , plz see – user534210 Apr 06 '18 at 21:26
@user534210 No need to post another question for the topologists' sine curve because the community will soon mark it as a duplicate of the same question. – GNUSupporter 8964民主女神地下教會 Apr 06 '18 at 21:30
1

I think you 'classic proof' needs a little work. Uh, for your '... and $\gamma$ be a continuous path' - is the constant path OK? – CopyPasteIt Apr 07 '18 at 14:08
@MikeMathMan Thanks for spotting out a loophole in my proof. To apply the pullback argument, $\gamma$ has to be a continuous path linking the disjoint pieces $U$ and $V$. – GNUSupporter 8964民主女神地下教會 Apr 07 '18 at 14:17

score 2 · Answer 2 · answered Apr 06 '18 at 20:32

Yes, the union is path connected, thus it is connected.

Note that if you have two points in the union you can always connect them with a path.

In case that both points are on the line or both are in the disk the path is just a segment connecting the points.

In case that one is inside the disk and the other on the line you connect the points to the point (1,0) and the path is the union of two segments.

score 0 · Answer 3 · answered Apr 08 '18 at 14:51

The OP's headline question wants to know if a subspace of $\mathbb R^2$ is connected, but then in the detailed posts asks

... does pathwise connectedness implies connectedness?

But they also state

... I can join any two points of X by a path (line) which lies inside this set ...

Here we will solve the problem directly, in term of 'pure' point-set topology; it won't be necessary to use the concept of a function.

To define the topological product of two spaces we specify a 'cartesian product' base. For $\mathbb R^2$ it is not difficult to show that a different base can be chosen that generates the result - we can use open disks.

Exercise: Show that all lines and line segments (can be either open or closed at an endpoint) in $\mathbb R^2$ are connected.

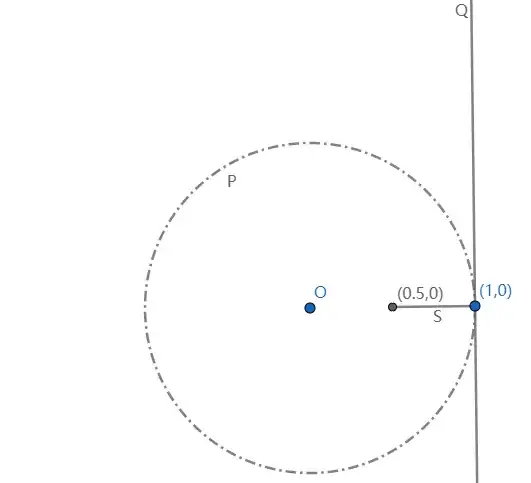
Let $(L_\alpha)$ be the family of all lines passing through the point $(1,0)$. Let

$\tag 1 S_\alpha = L_\alpha \bigcap X$

It is easy to see that each $S_\alpha$ is a line ($x = 1$) or a line segment. Moreover,

$\tag 2 \bigcup S_\alpha =X$ and $\tag 3 \bigcap S_\alpha = \{(1,0)\}$

But a well known result allows us to now conclude that $X$ is connected.

Let $P = \{(x,y) \in \mathbb R^2 : x^2+y^2<1 \}$ and $Q = \{(1,x) : x \in \mathbb R\}$. Is $X=P \cup Q$ connected?

3 Answers3