I would use the Projected Gradient Descend for this case.
Though the problem isn't Convex it will work nicely.
The algorithm is as following:
- Calculate the Gradient at the current point.
- Update the solution $ x = x - 2 t M x $ where $ 2 M x $ is the Gradient of the Objective Function and $ t $ is the step size.
- Project the output of previous step into $ {\mathbb{R}}_{+} $ by $ {x}_{i} = \max \left\{ {x}_{i}, 0 \right\} $.
- Project the output of previous step onto the Unit Sphere by $ {x}_{i} = \frac{ {x}_{i} }{ \left\| x \right\|_{2} } $.
- Go back to (1) (Or check validity of the point, KKT will do even the problem isn't Convex).
In a simple 2D example I created which worked pretty well:
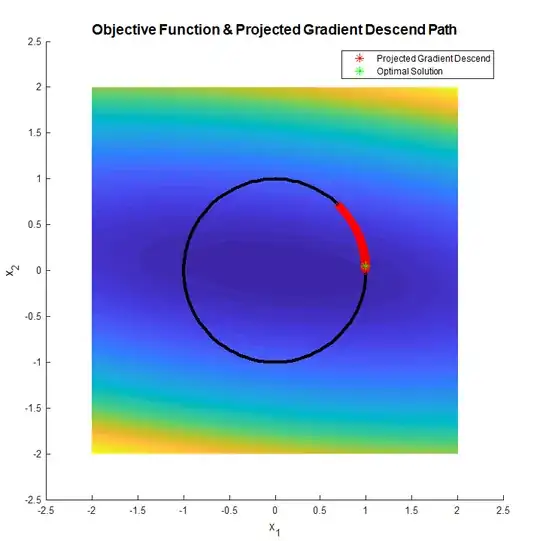
The code is available at my StackExchange Mathematics Q2699867 GitHub Repository.
Remark 001
I'd even considering starting with the solution of the Convex Problem when you replace the equality constraint $ \left\| x \right\|_{2} = 1 $ by $ \left\| x \right\|_{1} = 1 $ (This will make the problem basically constraining $ x $ to the Unit Simplex). You can either use it as a starting point for the above algorithm or approximated solution by itself.
Remark 002
Another approach might be something like I did in - Solution for $ \arg \min_{ {x}^{T} x = 1} { x}^{T} A x - {c}^{T} x $.
Yet after each iteration of updating $ \lambda $ you should also project the output $ x $ into $ \mathbb{R}_{+} $.
