Taking a quotient of the 1-sphere by identifying diametrically opposite points

Question

I have been working on the following problem:

"Let $\sim$ be the equivalence relation on the unit circle $S^1$ defined by $x \sim -x$, $x \in S^1$. Show that $S^1/\sim$ is homeomorphic to $S^1$ and interpret geometrically."

I have applied the following two theorems:

"Let $X$ and $Y$ be spaces and $f:X \to Y$ a continuous function from $X$ onto $Y$. In order that the natural correspondence $h:X/\sim_f \to Y$ defined by $h([x])=f(x)$, $x \in X$ be a homeomorphism, it is necessary and sufficient that $Y$ have the quotient topology determined by $f$."

"Let $X$ and $Y$ be spaces and $f:X \to Y$ a continuous function from $X$ onto $Y$. If $f$ is either open or closed, then $Y$ has the quotient topology determined by $f$."

It's not hard to see that $f(x)=-x$ is continuous, surjective, and open, so that $S^1/\sim\,\,\cong S^1$ follows from there.

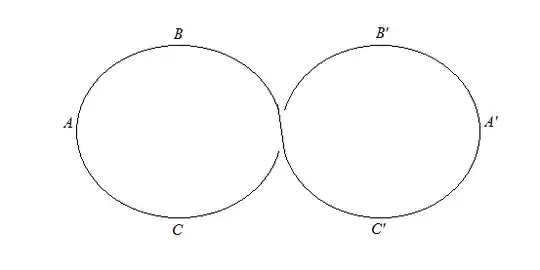
I'm having a difficult time picturing this geometrically. If we identify two opposite points on the circle, the resulting space would resemble a pinched-together circle, or figure-eight. I can't picture how pinching every pair of opposite points together yields the circle again. Could someone explain the geometric intuition behind this?

Answer 1

Imagine your circle lying in the $xy$-plane in $3$-space. Now pinch the points $(0,\pm1)$ together to the origin, giving, as you say, a figure-eight. Now take only the right-hand loop and, in space, rotate it $180$ degrees in the $x$-axis. Now take this loop and flip it, in space, through the $y$-axis; that is, fold it over so that all the picture is in the left-hand half-plane. If you follow what happened to any point originally at $(x,y)$ with $x>0$, you see that it lands on the point whose original coordinates were $(-x,-y)$. Voilà.

Answer 2

Let $\sim$ be the equivalence relation. I will identify $S^1$ with the set of complex numbers of modulus $1$.

• Consider the function $f:z\in S^1\mapsto z^2\in S^1$.
• It is clear that if $x$, $y\in S^1$ are such that $x\sim y$ then $f(x)=f(y)$, for in that case we have $x=\pm y$. This has the consequence that there is a function $\bar f:S^1/\mathord\sim\to S^1$ such that $\bar f([z])=z^2$ for all $z\in s^1$. Properties of the quotient topology imply at once that $\bar f$ is a continuous function. Check all this in detail!
• One can easily see that if $x$, $y\in S^1$ are such that $f(x)=f(y)$ then $x=\pm y$. This has as a consequence the fact that $\bar f$ is injective. Check this in detail!
• Finally, $\bar f$ is a surjective function —this is a consequence of the fact that $f$ itself is surjective.
• At this point, we got outselves a continuous bijection $\bar f:S^1/\mathord\sim\to S^1$.
• Now, there is a theorem which tells us that

a continuous bijection from a compact space to a Hausdorff space is an homeomorphism.

• Using this, we get that $\bar f$ is an homeo.

Answer 3

Start with a circle and fold it into a figure eight as shown above. Now fold it along the vertical centreline so that $A$ and $A'$ coincide, as do $B$ and $B'$, and $C$ and $C'$. You’ve now identified each point on the original circle with the point that was diametrically opposite it, and the result is a single circle.

Answer 4

If you identify antipodal points of the sphere $S^n$, you get $\mathbb{R}\mathbb{P}^n$. For $n=1$ you get $\mathbb{R}\mathbb{P}^1$, which is $S^1$ itself.

Answer 5

The way I think of it is, if you've identified every point with its antipode, then your original circle now has two copies of each point you care about. So let's throw away the duplicates and just keep half the points, giving you a semicircle. Except, oops, the two ends of the semicircle are also the same. So glue them together and you get a circle again.