5

This is from Angelo Vistoli’s notes http://homepage.sns.it/vistoli/descent.pdf page $71$.

Let $\mathcal{C}$ be a site and $\mathcal{U}=\{\sigma_i:U_i\rightarrow U\}$ be a covering of $U$. Let $\mathcal{F}$ be a fibered category over $\mathcal{C}$.

An object with descent data $(\{\xi_i\},\{\phi_{ij}\})$ on $\mathcal{U}$ is

  1. a collection of objects $\xi_i\in \mathcal{F}(U_i)$
  2. a collection of isomorphisms $\phi_{ij}:pr_2^*\xi_j\rightarrow pr_1^*\xi_i$ in $\mathcal{F}(U_i\times_U U_j)$

such that the following cocycle condition is satisfied. $$pr_{13}^*\phi_{ik}=pr_{12}^*\phi_{ij}\circ pr_{23}^*\phi_{jk}:pr_3^*\xi_k\rightarrow pr_1^*\xi_i$$

I do not understand the notation in this cocylce relation. Please explain what it means.

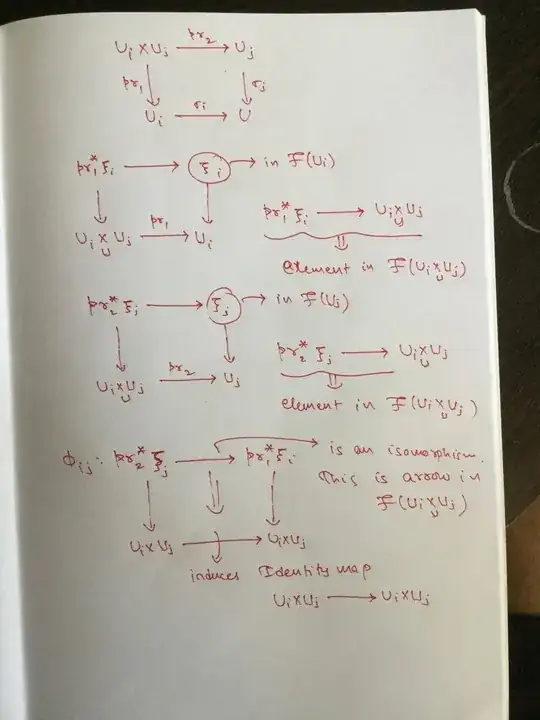
I am adding photo of diagrams relavent to the set up.enter image description here

  • 2
    I am using my iPad, so even typing math code is difficult and drawing commutative diagrams would take so much time. Please feel free to remove this photo and add the diagrams if you have enough time. –  Mar 16 '18 at 08:50

1 Answers1

2

So first we have the projections :

  • $pr_{12}:U_i\times U_j\times U_k\to U_i\times U_j$
  • $pr_{13}:U_i\times U_j\times U_k\to U_i\times U_k$
  • $pr_{23}:U_i\times U_j\times U_k\to U_j\times U_k$

These define functors $pr_{12}^*:\mathcal{F}(U_i\times U_j)\to\mathcal{F}(U_i\times U_j\times U_k)$ and similarly for $pr_{13}$ and $pr_{23}$.

Now $\phi_{ij}$ are morphisms between two objects $A$ and $B$ in $\mathcal{F}(U_i\times U_j)$. So we can apply the functor $pr_{12}$ to get a new morphism $pr_{12}^*\phi_{ij}:pr_{12}^*A\to pr_{12}^*B$. This will be a morphism in $\mathcal{F}(U_i\times U_j\times U_k)$.

You get similarly three morphisms $pr_{12}^*\phi_{ij}, pr_{13}^*\phi_{ik}$ and $pr_{23}^*\phi_{jk}$. The three of them being in the same category $\mathcal{F}(U_i\times U_j\times U_k)$.

What are their source and target ? $\phi_{ij}$ is a morphism $pr_2^*\xi_j\to pr_1^*\xi_i$, so pulling back you get $pr_{12}^*\phi_{ij}=pr_{12}^*pr_2^*\xi_j\to pr_{12}^*pr_1^*\xi_i$. But $pr_2pr_{12}:U_i\times U_j\times U_k\to U_k$ is the projection onto the second factor, and $pr_{12}^*pr_2^*=(pr_2pr_{12})^*$. So the source of $pr_{12}^*\phi_{ij}$ is $\xi_j$ pulled-back to $U_i\times U_j\times U_k$ through the second projection. So call it $pr_2^*\xi_j$, though here $pr_2$ means the second projection from the triple product $U_i\times U_j\times U_k$ onto the second factor.

Similarly you will have three morphisms :

  • $pr_{12}^*\phi_{ij}:pr_2^*\xi_j\rightarrow pr_1^*\xi_i$
  • $pr_{13}^*\phi_{ik}:pr_3^*\xi_k\rightarrow pr_1^*\xi_i$
  • $pr_{23}^*\phi_{jk}:pr_3^*\xi_k\rightarrow pr_2^*\xi_j$

Note that $pr_{12}^*\phi_{ij}$ and $pr_{23}^*\phi_{jk}$ can be composed to get a new morphism $$pr_{12}^*\phi_{ij}\circ pr_{23}^*\phi_{jk}:pr_3^*\xi_k\rightarrow pr_2^*\xi_j\rightarrow pr_1^*\xi_i$$

The cocycle condition is that this composition is equal to $pr_{13}^*\phi_{ik}$.

A quick note to get your hand on this : I recommend to write all of this using the topological notion of restriction. Instead of $pr_{12}:U_i\times U_j\times U_k\to U_i\times U_j$, think about the inclusion of $U_i\cap U_j\cap U_k\subset U_i\cap U_j$. So instead of writing $pr_{12}^*\xi$, write $\xi|_{U_{ijk}}$.

All of this can be written as follow :

  • take objects $\xi_i\in\mathcal{F}_{U_i}$
  • isomorphisms $\phi_{ij}:\xi_i|_{U_i\cap U_j}\to \xi_j|_{U_i\cap U_j}$
  • such that on the triple intersection $U_{ijk}=U_i\cap U_j\cap U_k$ : $\phi_{ik}|_{U_{ijk}}=\phi_{ij}|_{U_{ijk}}\circ \phi_{jk}|_{U_{ijk}}$ as morphisms $\xi_k|_{U_{ijk}}\to\xi_i|_{U_{ijk}}$.
Roland
  • 13,115
  • 1
  • 37
  • 39
  • I have seen this kind of cocylcle conditions in case of schemes and also in case of vector bundles. I was not very comfortable with the notion that given an arrow $U\rightarrow V$ in $\mathcal{C}$ this defines a functor among the categories $\mathcal{F}(V)\rightarrow\mathcal{F}(U)$ where $\mathcal{F}(U)$ is fiber of $U$ and similarly for$V$. This answer gives me one more reason to go back and understand this concept. Thanks. Everything is clear. –  Mar 16 '18 at 13:48
  • Do we really have $pr_{12}^pr_2^=(pr_2pr_{12})^*$ here? Or would this only hold up to some isomorphism? – Arnaud D. Mar 16 '18 at 14:39
  • @ArnaudD. Yes of course this is only up to an isomorphism $\alpha_{g,f}:f^g^\simeq (gf)^*$. There is coherence relations between different $\alpha_{hg,f}, \alpha_{h,gf}...$ I skipped this part for more readability since it is a first course (and in practice, very few people bother to write them all completely). But you are right, this is not a strict equality. – Roland Mar 16 '18 at 19:29
  • I have little difficulty in recalling the notation and I am not able to find my notes.... For $\xi_i\in \mathcal{F}(U_i), we have $pr_1^(\xi_i)$ and for $\xi_j\in \mathcal{F}(U_j), we have $pr_2^(\xi_j)$... Then they say there is an isomorphism $\phi_{ij}:pr_2^(x_j)\rightarrow pr_1^(x_i)$.... Is it that there always exists an isomorphism between $pr_2^(x_j)$ and $pr_1^(x_i)$ and we choose one such and name it $\phi_{ij}$ or, we are assuming there exists an isomorphism and naming it $\phi_{ij}$... –  Jul 04 '18 at 05:42
  • The isomorphisms $\phi_{ij}:pr_2^(x_j)\to pr_1^(x_i)$ is part of the descent data, its existence is not guaranteed, nor is its uniqueness. Think about sheaves on a topological space $X$, you are given sheaves on open subsets ${U_i}$ and you want to glue them together. Of course you need that the sheaf defined on $U_i$ and the sheaf defined on $U_j$ "agree" on $U_i\cap U_j$, and this won't be automatic. But you can't require that they are equal on $U_i\cap U_j$, this is too strong, you can only require that there exist an isomorphism. Also there are often many, and you need to choose one... – Roland Jul 04 '18 at 06:57