0

I was given the following triangle with the following initial values:

<img src="https://i.sstatic.net/REBbR.jpg">

As I started solving I arrived at the following:

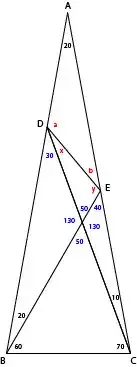
<img src="https://i.sstatic.net/USMNR.jpg">

To find $x$ can I use the following rule? The opposite angles of a quadrilateral sum up to $180°$, thus

$$x + 30 + 70 + 10 = 180\\ x = 70$$

Is my answer correct?

Blue
  • 83,939
Anirudh Murali
  • 13
  • 1
    The opposite angles of a quadrilateral only sums up to 180 degrees if the quadrilateral is concyclic (i.e., the four vertices lie on the same circle) – Lazy Lee Mar 14 '18 at 01:10
  • 1
    and just from looking at the graph, $x$ looks smaller than the 30 degrees that's right next to it, so intuitively it's hard to justify an answer like $x=70$. – Lazy Lee Mar 14 '18 at 01:11
  • Take a quadrilateral $ABCD$ where $AB = 3$ and $AB$ is perp to $BC$ And $BC$ is perp to $CD$ and $CD = 5$. Do the opposite angles add to 180? – fleablood Mar 14 '18 at 01:12
  • 1
    You;ll need to use trig. You equations are not linearly independent and they will not be solvable by algebra. – fleablood Mar 14 '18 at 01:24
  • Law of sines: $\sin (x + 30)$ over BE equals $\sin 20$ over DE. etc. mash them all out. Something will have to give. – fleablood Mar 14 '18 at 01:30

1 Answers1

1

No, it is incorrect. The geometrical way is quite hard to find, but you have to recognize some patterns.

Doing angle addition in this problem is of no use, to spare you some torture.

In the end, I gave up doing this problem, and used the cheap way (Law of Sines, Law of Cosines) to find the answer. However, here are some hints on how to approach the problem (after I found out the geometrical solution):

  1. Draw a line parallel to $BC$ which intersects $E$ ($EG$)
  2. Draw a line from $G$ to $C$ ($GC$), and label the intersection it has with $BE$ point $H$.
  3. Connect $A$ to $H$ (should automatically come to you)

Draw this out in a BIG image, and if you stare at one part of the image, everything should fall in place. Or, maybe you'll have to find several critical angles.

Hint: There are many equilateral triangles (as well as some isosceles triangles).