2

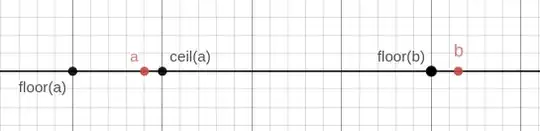
Let us define $\{t\} = t - \lfloor t \rfloor$ this is also sometimes referred to as frac$(t)$.

With this in mind how would I calculate $$I := \int_a^b f(\{t\}) dt$$ for some function $f$?

I ask because I'm trying to apply Euler-Maclaurin summation to $\zeta(s)$ and am stuck working with $$\int_a^b B_1(\{t\})g'(t)dt$$ where $B_1(x)$ is the first Bernoulli polynomial.

I'm trying to simplify this using integration by parts. But as I said stuck on how the $\{t\}$ effects the integral. It also may be beneficial to split the integral up as such: $$\int_a^b = \int_a^{a+1} + \int_{a+1}^{a+2} + \cdots + \int_{b-1}^b$$

Any help greatly appreciated!

kingee
  • 241

1 Answers1

2

First, assume $\lfloor a\rfloor\lt\lfloor b\rfloor$.

Diagram

\begin{eqnarray} \int_a^b f(\{t\}) dt&=&\int_{\{a\}}^1f(t)\,dt+\left(\lfloor{b}\rfloor-\lceil{a}\rceil\right)\int_0^1f(t)\,dt+\int_0^{\{b\}}f(t)\,dt\\ &=&\int_{0}^{1}f(t)\,dt+\int_{\{a\}}^{\{b\}}f(t)\,dt+\left(\lfloor{b}\rfloor-\lceil{a}\rceil\right)\int_0^1f(t)\,dt\\ &=&\int_{\{a\}}^{\{b\}}f(t)\,dt+\left(\lfloor{b}\rfloor-\lceil{a}\rceil+1\right)\int_0^1f(t)\,dt\\ &=&\int_{\{a\}}^{\{b\}}f(t)\,dt+\left(\lfloor{b}\rfloor-\lfloor{a}\rfloor\right)\int_0^1f(t)\,dt \end{eqnarray} Notice that this also works if $\lfloor a\rfloor\ge\lfloor b\rfloor$.

John Wayland Bales
  • 22,294
  • Thank you, substitution seems obvious now. So if $a, b \in Z$ if I split the integral up to $$\int_a^b = \int_a^{a+1} + \int_{a+1}^{a+2} + \cdots + \int_{b-1}^{b}$$ when I make the substitution in each of these $x \rightarrow t - \lfloor t \rfloor$ i have $dx/dt = 1$ since $\lfloor t \rfloor $ is constant in each case...? – kingee Mar 05 '18 at 17:22
  • That should do it. – John Wayland Bales Mar 05 '18 at 22:14
  • Thanks, very helpful – kingee Mar 06 '18 at 22:41