It might be obvious that $2\sqrt { 2\sqrt { 2\sqrt { 2\sqrt { 2\sqrt { 2\sqrt { \cdots } } } } } } $ equals $4.$ So what about $i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { \cdots } } } } } } \text{ ?} $ The answer might be $-1$, but I'm not sure as $i$ is not a real number. Can anyone help?
-
17It depends on which branch cut of $\sqrt{\cdot}$ you take, but under the principal branch cut $(-\infty, 0]$ and with the recursive formula $z_0 = i$, $z_{i+1} = i\sqrt{z_n}$ we have $\lim z_n = -1$. – Sangchul Lee Mar 01 '18 at 21:15
-
16The two highest-voted answers (as of writing) are incorrect because they do not show that the expression even has a limit, only that if the limit exists then it is $-1$. – Mar 02 '18 at 04:31
-
42How is the first claim obvious? Why do you think the answer "might be $-1$"? What's up with the title? – JiK Mar 02 '18 at 06:16
-
7@JiK is right: this question needs to be retooled from soup to nuts. This isn't comp.ai.philosophy. – eric Mar 02 '18 at 13:53
-
@Rahul does my answer show that, or is something still missing? – LLlAMnYP Mar 02 '18 at 14:28
-
Technically this notation is not correct, because if so, the computation will never begin (you cant write the initial value for the recurrence equation for this expression). It has to be $\ldots2\sqrt{2\sqrt{2}}$ – klimenkov Mar 02 '18 at 15:55
-
Why are you surprised that some expression with complex numbers is real? Like $i^4/i^2 = -1$... – Martín-Blas Pérez Pinilla Mar 02 '18 at 22:56
-
Maybe we can remove the title, which indicates nothing about the question and suggests a very different question. – Caleb Stanford Mar 03 '18 at 01:18
-
@6005 is there some consensus (somewhere on meta, perhaps) as to what the title of a question should be? I rather liked the old one and probably wouldn't have clicked on the new one. Many scientific journals seem to accept rather creative titles for papers ("The rise of graphene" comes to mind). – LLlAMnYP Mar 05 '18 at 11:01
-
@LLlAMnYP The official policy is that titles should clearly describe the question being asked. Of course there are many people who don't always follow it, including users like you who enjoyed this question title, and ultimately it is up to the community. Personally, I hate click-bait titles because I have no idea what I'm clicking on until I click on it. FWIW I also hate creative titles for papers (in my field). – Caleb Stanford Mar 05 '18 at 14:51
-
Actually, creative titles are one thing -- this one is a bit worse, having been deliberately misleading. I think we could probably find a consensus on meta that deliberately misleading titles are not good. But I don't have time to search around. – Caleb Stanford Mar 05 '18 at 14:52
-
@6005 perhaps the intent of the asker was in fact to ask a very different question: why does an expression with only imaginary subexpressions turn out to be real-valued? But it was an interesting problem all the same. – LLlAMnYP Mar 05 '18 at 14:59
-
When you take the square root of a positive real number, the result is closer to 1. Repeating gets you ever closer to 1. (This is useful for calculating logarithms on a five-banger calculator.) The same thing happens to negative reals and complex numbers. – richard1941 Mar 12 '18 at 15:27
7 Answers
\begin{eqnarray*} x= a\sqrt { a\sqrt { a\sqrt { a\sqrt { a\sqrt { a\sqrt { \cdots } } } } } } \\ x=a^{ 1+1/2+1/4+1/8+\cdots} \\ x=a^2 \end{eqnarray*} So it would seem that \begin{eqnarray*} i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { \cdots } } } } } }=\color{red}{-1}. \end{eqnarray*}
- 37,323
-
10That's got to be the best imaginary root series I have ever seen. - So it would seem. – ClassicEndingMusic Mar 02 '18 at 02:49
-
I don't know if it's absolutely correct, but I am posting it.
If we write $i $ as $e^{i\pi/2} $, then the given series becomes:
\begin{align} & e^{i\pi/2} \sqrt{e^{i\pi/2}\sqrt{e^{i\pi/2}\sqrt{e^{i\pi/2}\sqrt{e^{i\pi/2}} \cdots}}} \\[8pt] = {} & e^{i\pi \left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8} \cdots \right)} \\[8pt] = {} & e^{i\pi \left( \frac{1/2}{1-1/2} \right)} \\[8pt] = {} &\boxed{e^{i\pi}=-1} \end{align}
-
2@IwillnotexistIdonotexist But you don't even need it as seen in Michael's answer. – M. Winter Mar 02 '18 at 13:17
-
17You never even use the $e^{i\pi/2}$ representation, you could just as well have used $i$ and $i^2$ instead. – KarelPeeters Mar 02 '18 at 16:08
-
8Why does this have so many upvotes? The transformation to/from circular coordinates is completely superfluous, it serves no purpose. – BlueRaja - Danny Pflughoeft Mar 02 '18 at 19:11
-
4@BlueRaja-DannyPflughoeft On the contrary, I think it serves a very important purpose for the OP, who is uncertain about the relationship between real and complex numbers. A proof that exploits the key relationship between them (Euler's formula) is therefore essential from an algebra point of view. But what's more, this answer exposes a lovely geometric interpretation: The composition of rotations by 1/4, 1/8, 1/16... turns around the circle is 1/2 turns (a 180 degrees turn, a negation). Many other answers instead simply affirm the OP's own answer while relying on knowledge unavailable to OP. – Iwillnotexist Idonotexist Mar 02 '18 at 19:28
Let $z = r e^{i\theta} \in \mathbb{C}$ and $(z_n)_{n \geq 0}$ be defined by
$$ z_0 = z, \qquad z_{n+1} = z \sqrt{z_n} $$
where $\sqrt{\cdot} = \exp(\frac{1}{2}\log(\cdot))$ is the principal square root. In particular, if we define $m : \mathbb{R} \to \mathbb{R}$ by
$$ m(x) = \begin{cases} x, & \text{if } x \in (-\pi, \pi] \\ m(x + 2\pi) & \text{for all } x \in \mathbb{R} \end{cases} $$
then it follows that $\sqrt{re^{i\theta}} = \sqrt{r}e^{im(\theta)/2}$. So if we write $z_n = r_n e^{i\theta_n}$, then
$$ r_n = r^{2 - 2^{-n}}, \qquad \theta_0 = \theta, \qquad \theta_{n+1} = \theta + \frac{1}{2}m(\theta_n) $$
As a consequence,
If $|\theta| \leq \frac{\pi}{2}$, then we can inductively show that $\theta_n = (2 - 2^{-n})\theta \in (-\pi, \pi)$ and hence
$$ z_n \xrightarrow[n\to\infty]{} r^2 e^{2i\theta} = z^2. $$
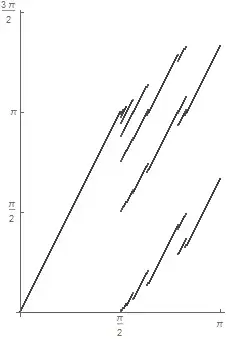
Now consider the case $\theta = \frac{2\pi}{3}$. Then we can show that $(\theta_n)$ has 3 limit points $\frac{4 \pi}{21}, \frac{16\pi}{21}, \frac{21 \pi}{21}$. This in particular tells that $z_n$ does not converge as $n\to\infty$. This kind of behavior is general for $\theta \in (\frac{\pi}{2}, \pi]$, as we see from the graph of $\theta$ versus limit points of $(\theta_n)$.
This tells that $i\sqrt{i\sqrt{i\sqrt{i\cdots}}} = i^2 = -1$ is sort of an 'edge case'.
- 181,930
By the same way it means: $$i^{1+\frac{1}{2}+\frac{1}{4}+\cdots}=i^2=-1.$$
- 203,855
-
Can someone to explain me what is a different between my solution and the Donald Splutterwit's solution? By the way, I posted my solution before. Thank you! – Michael Rozenberg Mar 02 '18 at 13:12
-
4
-
2You have my sympathies. :-) But since you asked: not only is the other answer more visually arresting, this one also requires the reader to scroll up and re-read the question. (E.g. it starts with “by the same way”: which way?) (And even the meaning of “it” refers to an expression that occurs in the question.) The other answer makes a statement that stands independently (you can read it and gain something from it even if you have forgotten the question). Such answers tend to be easier to read, especially if the reader has read other answers between reading the question and this one. – ShreevatsaR Mar 02 '18 at 22:45
One way to approach this fixed-point problem rigorously is to use the polar form of complex numbers. Consider the action of the mapping $$z\mapsto a\mathrm{e}^{\mathrm{i}\alpha}\sqrt{z}$$ when $z=r\mathrm{e}^{\mathrm{i}\phi}$ is expressed in polar form, $r>0$, $a>0$, $-\pi/2\leq\alpha\leq\pi/2$, $-\pi<\phi<\pi$. Under this mapping $$\begin{align}\ln r&\mapsto \tfrac{1}{2}\ln r+\ln a\\ \phi&\mapsto \tfrac{1}{2}\phi+\alpha\end{align}$$ Since this is a contractive mapping, it has a unique fixed point which must be $(\ln r,\phi)=(2\ln\alpha,2a)$. The result follows from letting $a=1$ and $\alpha=\tfrac{\pi}{2}$.
- 9,458
The two highest-voted answers (as of writing) are incorrect because they do not show that the expression even has a limit, only that if the limit exists then it is −1. – Rahul
We have the sequence
$$ a_0 = i,\quad a_{n+1} = i \sqrt{a_n}. $$
I think the other answers have sufficiently covered that the argument of each element of the sequence lies in $(0, \pi)$, so we can be sure that we're always taking the principal square root. They also have shown clearly enough (except for off-by-one errors) that
$$ a_n = \exp(i\pi - i\pi/2^n).$$
I assert that the limit of this sequence is $-1$. For any $\varepsilon>0$ there exists $N$ such that $|-1 - a_n| < \varepsilon$ when $n>N$.
$$| -1 - a_n |=| -1 - \exp(i\pi)\exp(-i\pi/2^m) |=| -1+\cos(\pi/2^n)+i\sin(\pi/2^n)|$$ which is less than or equal to
$$ |1 - \cos(\pi/2^n)| + |\sin(\pi/2^n)|. $$
$1-\cos(x)<x$ for all $x>0$, as is $\sin(x)<x$. So the above is less than $2\pi/2^n$. Then for $N > \log_2(2\pi/\varepsilon)$ we have $|a_n+1|<\varepsilon$.
- 231
Let $$x=i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { \cdots } } } } } }$$ $$\implies x^2=-1i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { i\sqrt { \cdots } } } } } }$$ $\implies x^2=-x$ $\implies x^2+x=0$ $\implies x(x+1)=0\implies x=0\; \text{or} -1$ since $x$ cannot be $0$, hence $x=-1$
- 622