1

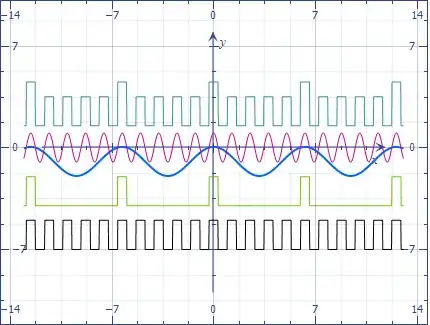
I am trying to model a gear with a gear tooth defect in the MATLAB/Simulink Simscape-environment. A tooth defect appears as an momentarily loss in gear meshing stiffness, which can be implemented in the model by modeling a square wave signal with a decrease of the signal value at the instant when the defect tooth meshes with a tooth on the opposing gear. The loss in meshing stiffness is present at every revolution of the gear. So, for a gear with five teeth and a defect at one of the teeth, every fifth mesh will appear as a loss in meshing stiffness, and thus, a decrease in the square wave signal.

The square wave signal has a maxima at the maximum meshing stiffness, $k_{max}$, and a minima at the minimum meshing stiffness, $k_{min}$. At the defect, both $k_{max}$ and $k_{min}$ gets subtracted by $\Delta k_{loss}$. The frequency of the function is obtained by multiplying the angular velocity $\omega$ of the gear by the number of teeth $N$, so that $f=\omega N$. The function I am trying to find is shown graphically in this figure.

This can be done in MATLAB by using two square functions with different duty cycles as follows,

A*square(f*t, 50) - A_flt*square(f*t/N, 100/N) + z;

where

$$A = \frac{k_{max}-k_{min}}{2}$$

$$A_{flt}= \frac{\Delta k_{loss}}{2}$$

$$z = A - A_{flt} + k_{min}$$

However, by using Simscape as the modeling environment, I am not allowed to use MATLAB functions directly. Thus, I have to do this purely by math. The square wave signal, without meshing losses, can be made by using a signed sine function, given as,

$$A*sgn(sin(ft))+z$$

where

$$z = A + k_{min}$$

I figure that subtracting the function by another periodic function with different duty cycle as in the MATLAB code, or making $z$ a periodic function that decreases by $\Delta k_{loss}$at every $n^{th}$ period and stays constant for the rest of the time, would leave me with my desired function. However, I can't seem to figure out how this can be done. Does anyone know a good approach to this problem?

dagfinae
  • 21
  • What is it that you want to achieve with your formula? If you are interested in describing the graph to a person without showing them the figure, it is not even necessary to to use sine functions, you could for example say that the graph assumes a constant value $a_k$ in the intervals $(fk,f(k+1))$ ($k\in \mathbb{N}$) and then specify $a_k$ by considering different cases for $k$ (say divisible by $5$ and so on). – Jan Bohr Mar 01 '18 at 13:09
  • The square wave function is used to describe the meshing stiffness in a spur gear, where $k_{max}$ is the maximum gear meshing stiffness and $k_{min}$ is the minimum gear meshing stiffness. Under a gear fault, for instance a tooth defect, the meshing stiffness is assumed to decrease. So, for a gear with five teeth and a defect at tooth number five, every fifth mesh will appear as a loss in meshing stiffness. The frequency of the function is obtained by multiplying the angular velocity $\omega$ of the gear by the number of teeth $N$, so that $f = \omega N$. – dagfinae Mar 01 '18 at 13:20
  • This does not answer my question. As far as I understand your question, you want to find a neat formula to describe a function with a given graph. That itself does not solve any problem, so I want to know what you are planning to do once you have such a neat formula. – Jan Bohr Mar 01 '18 at 14:08
  • Yes, that is sort of what I'm trying to do. When I have the formula I am able to implement this gear tooth defect in a gearbox model in MATLAB/Simulink, which is my problem. I have managed to do so by using the MATLAB function 'square' with different duty cycles, but I am modeling the gearbox in the Simscape environment, which does not allow me to use functions from the MATLAB library. – dagfinae Mar 01 '18 at 14:35
  • In that case you should edit your question and make clear that you are looking for a good way to implement this in matlab/simulink. The way I would do this in matlab would be to define my own function by fist checking in which interval $(fk,f(k+1))$ a given time $t$ lies and then assign a value depending on $k$ (see my first comment). But I am not an expert and there might be better ways. – Jan Bohr Mar 01 '18 at 14:51

1 Answers1

1

$$\cos t-a$$ changes sign in an interval of length $2\arccos a$ twice per period.

By adjusting $a$, you can obtain square waves of arbitrary duty cycle.

Now you can add the symmetric square wave of period $T$ and one of period $NT$ and duration $T$ or $\dfrac T2$ to achieve the desired effect.

enter image description here

  • I see how this might work, if I understand it right. If I add $sign(sin(ft))$ and $sign(sin(\frac{ft}{N}))-a$ and adjust $a$, I get a function that resembles what I am trying to achieve. However, this function needs to be tuned as parameters change, which will be a problem. For instance, the angular velocity $\omega$ is not necessarily constant. Is this the case, or do I misunderstand what you are trying to explain? – dagfinae Mar 01 '18 at 17:42
  • @dagfinae: "which will be a problem": why ? –  Mar 01 '18 at 17:43
  • Because I have to adjust $a$ graphically, and the "peak" will be phase shifted as the angular velocity changes. – dagfinae Mar 01 '18 at 18:00
  • @dagfinae: this is not a problem, adjust the relevant parameters. –  Mar 01 '18 at 18:05
  • Can you explain how? I can not manually adjust parameters while the model is running, so graphical adjustment of $a$ is not possible. – dagfinae Mar 01 '18 at 18:09
  • @dagfinae: what's the problem adjusting $a$ automatically ? Did you read my answer ? –  Mar 01 '18 at 18:10
  • Yes, I read your answer. The problem is that I do not understand how to adjust $a$ automatically. I have an equation that gives me the desired function. It is given as,

    $\frac{k_{max}-k_{min}}{2}sgn(sin(ft))-\frac{k_{loss}}{2}sgn(sin(\frac{ft}{N})-a)-\frac{k_{loss}}{2}sgn(sin(\frac{ft+\pi}{N}-a))$

    However, $a$ needs to be adjusted manually. For instance, $a=0.9511$ works for $N=5$, but not for $N=10$.

    If it is possible to express $a$ by the other parameters, so that it will be adjusted automatically, could you please explain how to do so?

     – dagfinae Mar 01 '18 at 18:58
  • @dagfinae: hem, it's explained in the first sentence ! –  Mar 01 '18 at 20:41
  • Okay, so obviously there's something I misunderstand here. I have the function $cos(t)-a$, which changes sign in an interval of length $2*cos^{-1}(a)$ twice per period.

    The interval I want is of length $\frac{1}{N}$ in terms of duty cycle, or $\frac{2\pi\omega}{N}$ in w.r.t. time. Thus, $2*cos^{-1}(a)=\frac{2\pi\omega}{N}$, which leaves me with $a=cos(\frac{\pi\omega}{N})$. Further, this leaves me with the function, $sgn(cos(\omega Nt)-sgn(cos(\omega t)-cos(\frac{2\pi\omega}{N}))$. This does not give the desired effect. Could you please provide an example of what you are trying to explain?

     – dagfinae Mar 02 '18 at 11:45