Projectile: $v^*w^*=gk$ for minimum launch velocity

Question

A projectile launched from $O(0,0)$ at velocity $v$ and launch angle $\theta$, passes through $P(k,h)$. The velocity of the projectile at $P$ is $w$. The slope of $OP$ is $\alpha$, i.e. $\tan\alpha=\frac hk$, and the length of $OP$ is $R$.

$\hspace{4cm}$

Let $v^*$ be the minimum launch velocity for the projectile to reach $P$, and $w^* $ the corresponding minimum terminal velocity at $P$. In the course of working out $v^*$, I noticed this neat relationship: $$\color{red}{\boxed{v^*w^*=gk}}\tag{1}$$

which can be proven easily using calculus. The relationship is interesting because of its symmetry and also its independence from $\theta$ and $h$. It also helps simplify the solution of projectile problems relating to minimum velocities, e.g. this question here.

Question 1: Is it possible to derive this relationship given by $(1)$ directly without using calculus but by exploiting some geometric or kinematic symmetry?

Separately, we know that, for a projectile for a given range $R$ (on the same level), the minimum launch velocity is given by $v^*=\sqrt{gR}$. Assume that, for another given range $r$, the minimum launch velocity is $w^*=\sqrt{gr}$. Substituting in $(1)$ gives $k=\sqrt{Rr}$, i.e. $k$ is the geometric mean of $R$ and $r$.

Question 2: Can the relationship given by $(1)$ be derived using the relationships between minimum launch velocity and range shown above, perhaps through a geometric transform of some sort?

Answer 1

Because $w_x=v_x$ and $v_y^2=w_y^2-2gh$, the minimum speed in the origin implies you arrive with the minimum possible speed to point $(k,h)$.

I think the following picture shows a symmetry which could be useful. The minimum possible speed to reach $(k,h)$ is attained when you throw the projectile in the direction bisecting the angle between the $OP$ line and vertical axis. Because this trajectory reaches $P$ with the minimum possible speed, it also solves the "reverse" problem (by reversing the velocity direction), that is, from $P$ to reach $O$ with minimum speed. Therefore, $\vec{w}$ also bisects the angle that $OP$ makes with $\hat{y}$ at $P$, and therefore $\vec{v}\perp\vec{w}$.

By the way, proving that the maximum range in a slope (or minimum speed to a fixed range) is attained in the bisecting direction is a classical and nice problem, and it can be done without using calculus as well (here, for example).

Following with the reasoning, we then have $$ \begin{align}|\vec{v}\times\vec{w}|^2&=v^2w^2\qquad;\vec{v}\perp\vec{w}\\ &=(v_x w_y-w_x v_y)^2\\ &=v_x^2(v_y-w_y)^2\qquad;|v_x|=|w_x|\\ &=v_x^2(g t_f)^2\qquad;\text{where $t_f$ is time of flight}\\ &=(v_xt_f)^2g^2=k^2g^2~~.\\ \end{align} $$

Answer 2

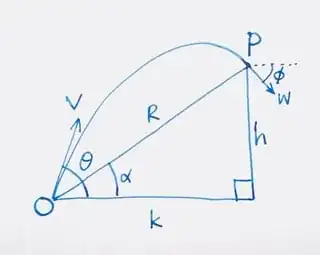
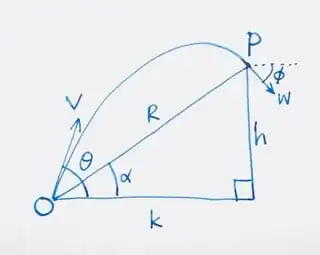
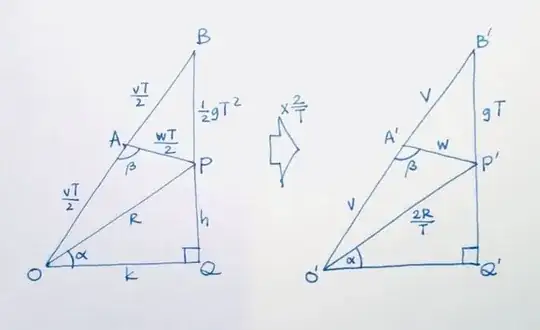
Consider projectile with parameters as shown in diagram below.

$\hspace{4cm}$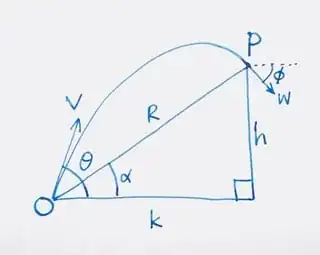

Let $T$ be the total time taken for the journey of the projectile, and $\beta$ be the angle between the initial and terminal velocities.

Refer to diagrams above. As the projectile is a motion under constant acceleration, it can be modelled as either

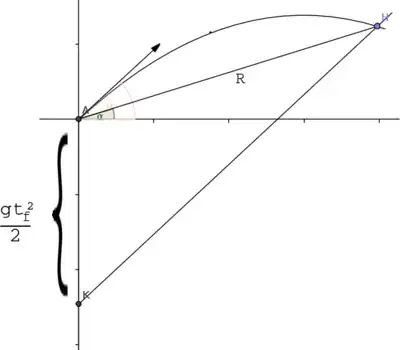
(a) First Scenario:-

• $(1)$ motion at constant velocity $\mathbf v$ from $O$ to $A$ for the first half of $T$ (distance travelled: $\frac {vT}2$),and
• $(2)$ motion at constant velocity $\mathbf w$ from $A$ to $P$ for the second half of $T$ (distance travelled: $\frac {wT}2$).

or

(b) Second Scenario**:- as a composite motion of the following:

• $(1)$ motion at constant velocity $\mathbf v$ from $O$ to $B$ for time $T$ (distance travelled: $vT$) and
• $(2)$ vertical free fall under gravity from $B$ to $P$ for time $T$ (distance travelled: $\frac 12gT^2$).

(NB - velocity here refers to a vector quantity, i.e. both speed and direction.)

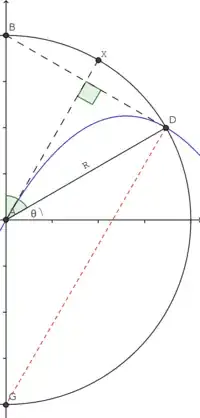
Consider the diagram on the right, which is the left diagram scaled by $\frac 2T$.

$$\begin{align} \triangle O'B'P'= \tfrac 12 \cdot 2v\cdot w\cdot \sin\beta &=\tfrac 12\cdot gT\cdot \tfrac {2R}T\cos\alpha \\ vw\sin\beta&=gR\cos\alpha\\ vw\sin\beta&=gk\\ \color{red}{v^*w^*}&\color{red}{=gk} \end{align}$$

As $g,k, $ are fixed, $v,w$ will be at a minimum when $\sin\beta$ is at a maximum, i.e. $\sin\beta=1 (\beta=\tfrac\pi2)$, hence $v^*, w^* $ are mutually perpendicular. Note that $w^2=v^2-2gh$ per energy conservation, and as $h$ is fixed, minimum $w^*$ corresponds to minimum $v^*$.

---

EARLIER SOLUTION (posted 21 March 2018)

For minimum velocity (i.e. minimum kinetic energy), $$\begin{align} {v^*}^2+{w^*}^2&=2gR\qquad\qquad\;\tag{1}\end{align}$$ where $^*$ indicates quantities corresponding to the minimum velocity case.
See Footnote for additional details.

Also, from conservation of energy ($V^2=U^2+2AS$), we have, for the general case, $$\begin{align} v^2-w^2&=2gh\color{lightgrey}{=2gR\sin\alpha}\tag{2}\end{align}$$

$\tfrac 12 \big((1)\pm (2)\big)$ : $${v^*}^2=g(R+h)\color{lightgrey}{=gR(1+\sin\alpha)}\\ {w^*}^2=g(R-h)\color{lightgrey}{=gR(1-\sin\alpha)}$$ and it follows that $$\begin{align} {v^*}^2{w^*}^2&=g^2(R^2-h^2)\color{lightgrey}{=g^2R^2(1-\sin^2\alpha)}\ \\&=g^2k^2\qquad\;\;\color{lightgrey}{=g^2R^2\cos^2\alpha}\\ \color{red}{v^*w^*}&\color{red}{=gk\;\blacksquare}\;\;\ \qquad\color{lightgrey}{=gR\cos\alpha}\end{align}$$

$\hspace{5cm}$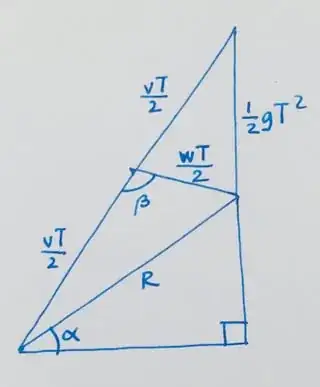

---

Footnote

Using the cosine rule twice,we have

$$\begin{align} R^2 &=\left(\tfrac {vT}2\right)^2+\left(\tfrac {wT}2\right)^2-2\left(\tfrac {vT}2\right)\left(\tfrac {wT}2\right)\cos\beta\qquad \tag{3}\\ \left(\tfrac 12 gT^2\right)^2 &=\left(\tfrac {vT}2\right)^2+\left(\tfrac {wT}2\right)^2-2\left(\tfrac {vT}2\right)\left(\tfrac {wT}2\right)\cos (\pi-\beta) \tag{4}\\ (3)+(4):\hspace{2cm}\\ R^2+\left(\tfrac 12 gT^2\right)^2 &=2\big(\left(\tfrac {vT}2\right)^2+\left(\tfrac {wT}2\right)^2\big) \\ v^2+w^2&=\tfrac 12 \left(g^2T^2+\tfrac {4R^2}{T^2}\right)\\ &=\tfrac 12\underbrace{\left(gT-\tfrac {2R}T\right)^2}_{\ge0}+2gR\\ &\ge 2gR\\ {v^*}^2+{w^*}^2&=2gR \end{align}$$ which is as used in equation $(1)$ above, with $^*$ indicating quantities corresponding to the minimum velocity case.

This occurs when ${T^*}^2=\tfrac {2R}g$, i.e. $\tfrac 12g{T^*}^2=R$. Using this and from the diagram we deduce that $\beta^*=\frac {\pi}2$, i.e. at minimum $v,w$, both $\mathbf v, \mathbf w$ are perpendicular to each other. This is shown in the diagram below.

$\hspace{4cm}$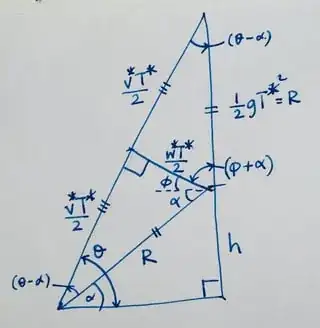

To deduce the values of $\theta$ and $\phi$, consider the triangles shown below.

$\hspace{4cm}$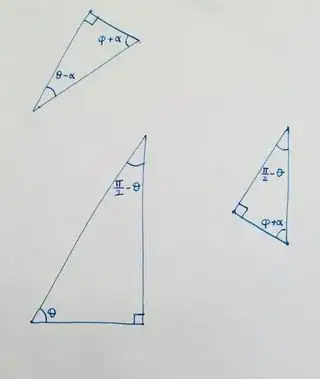

From first triangle, $$\begin{align} (\theta-\alpha)+(\phi+\alpha)&=\tfrac \pi 2\\ \theta+\phi&=\tfrac\pi 2\tag{5} \end{align}$$

From the lower two triangles,

$$\begin{align} (\tfrac\pi2-\theta)+(\phi+\alpha)&=\tfrac\pi2\\ \theta-\phi&=\alpha\tag{6}\\ \tfrac 12 \big((5)\pm (6)\big):\quad\qquad\\ \theta&=\tfrac\pi4+\tfrac\alpha2\\ \phi&=\tfrac\pi4-\tfrac\alpha2 \end{align}$$

which are launch and terminal angles corresponding to the minimum velocity case.

Conversely this also gives the well-known result, where the optimal launch angle to achieve maximum distance in direction $\alpha$ is one that bisects $\alpha$ and the vertical.

---

** An alternative Second Scenario would be a composite motion of the following:

• $(1)$ vertical launch at $gT$ under gravity for time $T$ (distance travelled: $\frac 12gT^2$), and
• $(2)$ motion at constant velocity $\mathbf w$ for time $T$ (distance travelled: $wT$) and

  ---

Alternative Interpretation

An alternative interpretation to the results might be given as follows. Refer to the diagram below.

$\hspace{3cm}$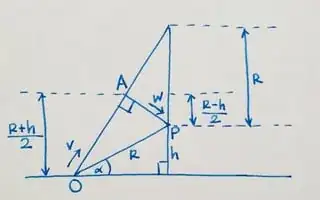

Let $A$ be the highest point reached by the particle under the scenario above where it travels half the time at constant initial launch velocity under zero gravity. The vertical distances from $A$ to $O,P$ are $\frac {R+h}2$ and $\frac {R-h}2$ respectively.

For a particle dropped from a height $H$ from the ground and falling vertically under gravity, its velocity upon reaching the ground is $\sqrt{2gH}$. Similarly, a particle under free fall of gravity, when launched vertically upwards at a velocity if $\sqrt{2gH}$, will reach a height of $H$. Here we refer to $\sqrt{2gH}$ as the vertical launch velocity for height $H$.

The magnitudes of the initial and terminal velocities of the projectile, $v^*,w^*$ are equal to the vertical launch velocities for heights $\frac {R+h}2, \frac {R-h}2$ respectively, i.e.

$${v^*}^2=2g\left(\tfrac {R+h}2\right)=g(R+h)\\ {w^*}^2=2g\left(\tfrac {R-h}2\right)=g(R-h)\\$$ which gives $${v^*}^2+{w^*}^2=2gR$$ and also $$v^*w^*=g\sqrt{R^2-h^2}=gk$$

---

MUCH EARLIER SOLUTION (Not so neat) (Posted 5 March 2018)

Note that $w^2=v^2-2gh$. Since $h$ is fixed, therefore minimum $w$ corresponds to minimum $v$.

Let $v^*, w^*$ be the minimum values of $v, w$ respectively. $$\begin{align} v^2w^2&=v^2(v^2-2gh)\\ &=v^2\left[v^2-2g\left(k\tan\theta-\frac {gk^2}{2v^2}(\tan^2\theta+1)\right)\right]\\ &=v^4-2gkv^2\tan\theta+g^2k^2\tan^2\theta+g^2k^2\\ &=\underbrace{\left(v^2-gk\tan\theta\right)^2}_{\ge 0}+g^2k^2\\ &\ge g^2k^2\\ \color{red}{v^*w^*}&\color{red}{=gk\qquad\blacksquare}\end{align}$$ This occurs when ${v^\ }^2={v^*}^2=gk\tan\theta$.

Additional Note

It can be shown that $\tan\theta=\dfrac {R+h}k$, where $R=\sqrt{k^2+h^2}$.

Hence $${v^*}^2=g(R+h)\\ {w^*}^2=g(R-h)$$

Answer 3

This is a complement to the previously posted answer. While solving this problem I realized that the set-up also serves to prove another interesting fact. That is, the flight times of the optimal trajectories to the target depend only on $R=\sqrt{h^2+k^2}$, independent of inclination.

In the second picture below, when the minimum energy projectile thrown from $A$ reaches $D$, a "projectile" released with zero velocity from $A$ will reach point $G$. In addition, projectiles thrown with parallel velocities (including zero velocity) from the point of origin at the same time remain forming a line parallel to the original velocity at all subsequent times. Therefore, $GD$ (being the line joining the projectiles at $G$ and $D$ at time $t_f$) is parallel to $AX$ (that is, $\vec{v}\parallel AX\parallel GD$), thus, $\angle{BDG}$ is a right angle and $G$ is also in the circumference. Therefore, the flight time for all minimum energy projectiles is the same as an object falling from $A$ to $G$, given by $\sqrt{\frac{2R}{g}}$.

Second, more explicit derivation

Using a bit of trigonometry, we show that the smallest initial velocity $\vec{v}$ of the projectile to reach a distance of $R$ in a direction forming an angle of $\alpha$ with the horizontal is attained when the $\vec{v}$ direction bisects the angle between the vertical and $\alpha$. Part of the interest of this answer is that it does not use calculus either.

First, we calculate the range of the projectile in the direction given by $\alpha$ when being thrown with an arbitrary velocity $\vec{v}$ forming an angle $\theta$ with the horizontal. Following the same reasoning as in the previous diagram, we deduce that is $KH\parallel\vec{v}$ (in the second picture below). We can immediately see that the $\angle AHK=\theta-\alpha$, and $$ \frac{gt_f^2}{2}= \frac{R\sin(\theta-\alpha)}{\cos\theta}~~.\tag{1}$$

Furthermore, it is also clear that, since there is no acceleration in the $\hat{x}$ direction, $$ R\cos\alpha=vt_f\cos\theta~~.\tag{2}$$ From (1) and (2) we deduce $$R=\frac{v^2}{g}\frac{2\cos(\theta)\sin(\theta-\alpha)}{\cos^2\alpha}=\frac{v^2}{g}\frac{(\sin(2\theta-\alpha)-\sin(\alpha))}{\cos^2\alpha}~~,\tag{3}$$ from where it is very clear that the maximum range is given by $2\theta-\alpha=\pi/2~~$ (or $\theta$ bisects the angle between $AH$ and the vertical). In turn, the maximum range is given by $\frac{v^2}{g(1+\sin\alpha)}$.

Concluding, by squaring (1) $$\begin{align} t_f^4&= \left(\frac{2R}{g}\right)^2\frac{\sin^2((\pi/2-\alpha)/2)}{\cos^2((\pi/2+\alpha)/2)}\qquad;\theta=(\pi/2+\alpha)/2\\ &=\left(\frac{2R}{g}\right)^2 \frac{\frac{1-\cos(\pi/2-\alpha)}{2}}{\frac{1+\cos(\pi/2+\alpha)}{2}}\\ &=\left(\frac{2R}{g}\right)^2 \frac{1-\sin\alpha}{1-\sin\alpha}\\ &=\left(\frac{2R}{g}\right)^2~~, \end{align} $$ therefore $t_f=\sqrt{\frac{2R}{g}}$, that is, the same result as in the first answer with $t_f$ independent of $\alpha$.

Answer 4

LATEST SOLUTION
(Using vectors)

$\hspace{5cm}$

Let $\mathbf v,\mathbf w$ be the initial (launch) and terminal velocity vectors of the projectile, and $\beta$ be the angle between them.
$\hspace{5cm}$

The projectile motion can be modelled as

(i) EITHER as a composite motion of the following:

• motion at constant velocity $\mathbf v$ for time $T$ (distance travelled: $vT$) and

• vertical free fall under gravity for time $T$ (distance travelled: $\frac 12gT^2$).

(ii) OR as a composite motion of the following:

• upward vertical launch at velocity $gT$ under gravity for time $T$ (distance travelled: $\frac 12gT^2$), and

• motion at constant velocity $\mathbf w$ for time $T$ (distance travelled: $wT$) and

Let $\mathbf R$ be the direction vector for $\vec{OP}$, and $\mathbf g$ the gravity vector.

Distance equations for both equivalent composite motions above are as follows:

$$\begin{align} \mathbf R&=\mathbf vT+\tfrac 12 \mathbf gT^2\tag{1}\\ \mathbf R&=\mathbf wT-\tfrac 12 \mathbf gT^2\tag{2}\\\\ \tfrac {(1)+(2)}T:\hspace {6.5cm} (\mathbf v+\mathbf w)&=\tfrac 2T \mathbf R\tag{A}\\ \tfrac {(1)-(2)}T:\hspace{6.5cm} (\mathbf v- \mathbf w) &= \mathbf gT\tag{B}\\\\ (\text A)\cdot (\text B):\hspace{5cm} (\mathbf v+\mathbf w)\cdot (\mathbf v-\mathbf w)&=2\mathbf R\cdot \mathbf g\color{lightgrey}{=2(R\sin\alpha) g}\\ v^2-w^2&=2gh\tag{I}\\\\ (\text A)\cdot (\text A):\hspace {1cm} (\mathbf v+\mathbf w)\cdot (\mathbf v+\mathbf w)=v^2+w^2+2vw\cos\beta &=\tfrac {4R^2}{T^2}\tag {IIa}\\ (\text B)\cdot (\text B):\hspace {1cm} (\mathbf v-\mathbf w)\cdot (\mathbf v-\mathbf w)=v^2+w^2-2vw\cos\beta &={g^2T^2}\tag {IIb}\\ \tfrac12\big((\text{IIa})+(\text{IIb})\big):\hspace{4.5cm} v^2+w^2\qquad \qquad \;\; &=\tfrac 12 \big(\tfrac {4R^2}{T^2}+g^2T^2\big)\\ &=\tfrac 12 \underbrace{\big(\tfrac {2R}T-gT\big)^2}_{\ge 0}+2gR\\ &\ge 2gR\\ {v^*}^2+{w^*}^2&=2gR\tag{II}\\ (T^*&=\tfrac{2R}g)\\\\ \tfrac 12 \big((\text{I})\pm(\text{II})\big):\hspace{7.5cm} {v^*}^2&=g(R+h)\\ {w^*}^2&=g(R-h)\\\\ {v^*}^2{w^*}^2&=g^2(R^2-h^2)=g^2k^2\\ \color{red}{v^*w^*}&\color{red}{=gk} \end{align}$$

---

Alternatively we can bypass steps (I), (II) and arrive at the required result directly from (A), (B) as follows:

$$ \begin{align} (\text{A})\times(\text{B}):\hspace{5cm} (\mathbf v+\mathbf w)\times (\mathbf v - \mathbf w) &=\tfrac 2T \mathbf R \times \mathbf gT\\ 2\big|\mathbf v\times \mathbf w\big| &=2\big|\mathbf R \times \mathbf g\big|\\ vw\sin\beta&=(R\cos\alpha)g\\ &=gk\\ \color{red}{v^*w^*}&\color{red}{=gk}\hspace{1cm} \end{align} $$ with minimum values of $v,w$ occuring when at maximum $\sin\beta(=1)$, i.e. at $\beta=\tfrac {\pi}2$.