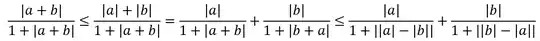Use Triangle Inequalities to Prove an Inequality

Question

Use the triangle inequalities to prove that:

$$\frac{|a+b|}{1+|a+b|}\le\frac{|a|}{1+|a|} + \frac{|b|}{1+|b|}$$ for all $a,b\in\mathbb{R}$.

I've made it this far, but it doesn't seem to be helping much; what I end up with at the end isn't very useful:

Clearly I'm taking a wrong turn somewhere, but I'm not sure what else to try. Any advice?

You aren't considering that $|a|+|b| \ge |a|$. So you are closer than you think. — fleablood, Feb 13 '18 at 05:43

score 4 · Accepted Answer · answered Feb 13 '18 at 05:37

4

$$\frac{|a+b|}{1+|a+b|}=1-\frac{1}{1+|a+b|}\leq1-\frac{1}{1+|a|+|b|}=$$ $$=\frac{|a|}{1+|a|+|b|}+\frac{|b|}{1+|a|+|b|}\leq\frac{|a|}{1+|a|}+\frac{|b|}{1+|b|}.$$

answered Feb 13 '18 at 05:37

Michael Rozenberg

203,855

Man, I should have known to try that considering the form it was written in. Thanks a bundle. – EllipticalInitial Feb 13 '18 at 05:38

Use Triangle Inequalities to Prove an Inequality

1 Answers1