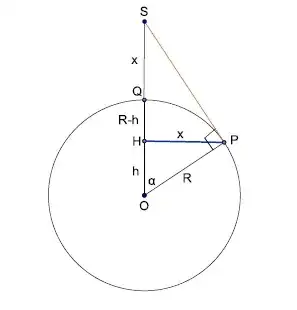
While trying to find the tribonacci cousin of this post, I came across this nice short article A Geometric Problem of Omar Khayyam and its Cubic by Wolfdieter Lang. Given the figure,
The problem is to find the point $P$ on a circle with radius $R$ such that,
$$\frac{x}{R} = \frac{R-h}{h}$$
By the Pythagorean theorem, we have $R^2 =h^2+x^2$. Eliminating $R$, we then get,
$$x^3-2hx^2+2h^2x-2h^3=0$$
If $h=10$, then $x^3+200x=20x^2+2000$, the cubic mentioned in Khayyam's MacTutor biography and this MSE post.
However, if $h=1$, then,
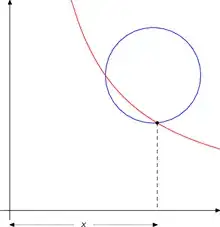
$$x^3-2x^2+2x-2=0$$
which, if this Wikipedia section is to be believed, was also solved by Khayyam using a circle and a hyperbola,
Remarkably, this real root is $\displaystyle x= \frac1T+1$ with tribonacci constant $T$. So Khayyam was playing with one of the $n$-nacci ratios before Fibonacci.
Q: This is the fourth geometric context I've seen where the tribonacci constant plays a role, after the snub cube, the hard hexagon model, and this short note. Are there other geometric contexts that the tribonacci constant appears in?
Update: A fifth geometric rendering is already given in an answer here: the tribonacci constant appears in the neusis construction of the regular hendecagon.