in the quadrilateral $ABCD$, $AC$ and $BD$ intersect in point $E$. if angles $\angle BDC=50^\circ$ , $\angle BCA=20^\circ$ , $\angle ACD=60^\circ$ and $\angle CAB=30^\circ$. Find $\angle BDA$.
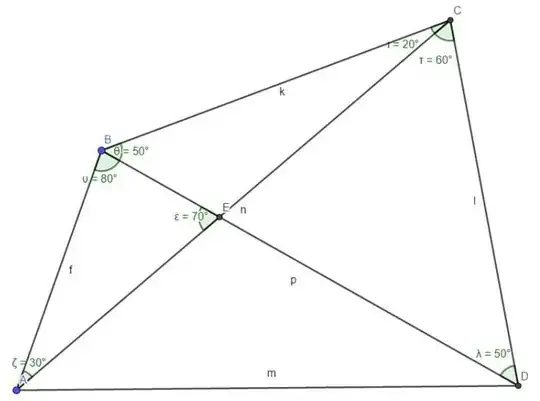
in the quadrilateral $ABCD$, $AC$ and $BD$ intersect in point $E$. if angles $\angle BDC=50^\circ$ , $\angle BCA=20^\circ$ , $\angle ACD=60^\circ$ and $\angle CAB=30^\circ$. Find $\angle BDA$.

By law of sines we obtain: $$\frac{ED}{EB}=\frac{ED}{EC}\cdot\frac{EC}{BE}=\frac{\sin60^{\circ}}{\sin50^{\circ}}\cdot\frac{\sin50^{\circ}}{\sin20^{\circ}}=\frac{\sin60^{\circ}}{\sin20^{\circ}}.$$ In another hand, $$\frac{ED}{EB}=\frac{ED}{AE}\cdot\frac{AE}{EB}=\frac{\sin(70^{\circ}-x)}{\sin{x}}\cdot\frac{\sin80^{\circ}}{\sin30^{\circ}}=2\sin80^{\circ}\left(\sin70^{\circ}\cot{x}-\cos70^{\circ}\right).$$ Thus, $$\cot{x}=\frac{\frac{\sin60^{\circ}}{2\sin20^{\circ}\sin80^{\circ}}+\cos70^{\circ}}{\sin70^{\circ}}=\frac{\sin60^{\circ}+2\sin^220^{\circ}\sin80^{\circ}}{2\sin20^{\circ}\cos10^{\circ}\cos20^{\circ}}=$$ $$=\frac{\sin60^{\circ}+(1-\cos40^{\circ})\sin80^{\circ}}{\sin40^{\circ}\cos10^{\circ}}=\frac{\sin60^{\circ}+\cos10^{\circ}-\frac{1}{2}\sin120^{\circ}-\frac{1}{2}\sin40^{\circ}}{\sin40^{\circ}\cos10^{\circ}}=$$ $$=\frac{\sin60^{\circ}+2\cos10^{\circ}-\cos50^{\circ}}{2\sin40^{\circ}\cos10^{\circ}}=\frac{\sin60^{\circ}+\cos10^{\circ}+2\sin30^{\circ}\sin20^{\circ}}{2\sin40^{\circ}\cos10^{\circ}}=$$ $$=\frac{\sin60^{\circ}+\sin80^{\circ}+\sin20^{\circ}}{2\sin40^{\circ}\cos10^{\circ}}=\frac{\sin60^{\circ}+2\sin50^{\circ}\cos30^{\circ}}{2\sin40^{\circ}\cos10^{\circ}}=$$ $$=\sin60^{\circ}\cdot\frac{1+2\sin50^{\circ}}{2\sin40^{\circ}\cos10^{\circ}}=\sin60^{\circ}\cdot\frac{\sin30^{\circ}+\sin50^{\circ}}{\sin40^{\circ}\cos10^{\circ}}=2\sin60^{\circ}=\sqrt3,$$ which gives $x=30^{\circ}.$
Take $O$ the circumcenter of $\triangle ABC$, see that $\triangle BCO$ is equilateral, $OA=OB=OC=BC=CD,\widehat{CAO}=\widehat{OCA}=40^\circ,\widehat{DCO}=20^\circ$, $\triangle OCD$ is isosceles, $\widehat{COD}=80^\circ=\widehat{CAO}+\widehat{OCA}$, i.e. $O$ lies onto $AD$. From here just angle calculus gives the answer, $\widehat{ADB}=30^\circ$.
From the triangle $\Delta ABD$, law of sines:
$\dfrac{\overline{AB}}{\sin\left(\angle{BDA}\right)}=\dfrac{\overline{AD}}{\sin {80^{\circ}}}\rightarrow\overline{AD}=\overline{AB}\cdot\dfrac{\sin{80^{\circ}}}{\sin\left(\angle{BDA}\right)}$
From the triangle $\Delta ACD$, law of sines:
$\dfrac{\overline{CD}}{\sin\left(\angle{CAD}\right)}=\dfrac{\overline{AD}}{\sin {60^{\circ}}}\rightarrow\overline{AD}=\overline{CD}\cdot\dfrac{\sin{60^{\circ}}}{\sin\left(\angle{CAD}\right)}$
Then,
$\overline{AB}\cdot\dfrac{\sin{80^{\circ}}}{\sin\left(\angle{BDA}\right)}=\overline{CD}\cdot\dfrac{\sin{60^{\circ}}}{\sin\left(\angle{CAD}\right)}$
keep this equation (1).
From the triangle $\Delta ABC$, law of sines:
$\dfrac{\overline{AB}}{\sin{20^{\circ}}}=\dfrac{\overline{BC}}{\sin {30^{\circ}}}\rightarrow\overline{BC}=\overline{AB}\cdot\dfrac{\sin{30^{\circ}}}{\sin{20^{\circ}}}$
From the triangle $\Delta BCD$ (isosceles), law of sines:
$\dfrac{\overline{CD}}{\sin{50^{\circ}}}=\dfrac{\overline{BC}}{\sin {50^{\circ}}}\rightarrow\overline{BC}=\overline{CD}$
Then,
$\overline{CD}=\overline{AB}\cdot\dfrac{\sin{30^{\circ}}}{\sin{20^{\circ}}}$
keep this equation (2).
Apply the second equation (2) on the first (1). Thus,
$\overline{AB}\cdot\dfrac{\sin{80^{\circ}}}{\sin\left(\angle{BDA}\right)}=\left(\overline{AB}\cdot\dfrac{\sin{30^{\circ}}}{\sin{20^{\circ}}}\right)\cdot\dfrac{\sin{60^{\circ}}}{\sin\left(\angle{CAD}\right)}$
$\sin\left(\angle{CAD}\right)\cdot\sin{20^{\circ}}\cdot\sin{80^{\circ}}=\sin\left(\angle{BDA}\right)\cdot\sin{30^{\circ}}\cdot\sin{60^{\circ}}$
$\sin\left(\angle{CAD}\right)\cdot\sin{20^{\circ}}\cdot\sin{80^{\circ}}=\sin\left(\angle{BDA}\right)\cdot \dfrac{\sqrt{3}}{4}$
Since $\angle{CAD}+\angle{BDA}=\angle{BEA}=70^{\circ}\rightarrow\angle{CAD}=70^{\circ}-\angle{BDA}$
So,
$\sin\left(70^{\circ}-\angle{BDA}\right)\cdot\sin{20^{\circ}}\cdot\sin{80^{\circ}}=\sin\left(\angle{BDA}\right)\cdot\dfrac{\sqrt{3}}{4}$
$\left[\sin{70^{\circ}}\cdot\cos\left(\angle{BDA}\right)-\sin\left(\angle{BDA}\right)\cdot\cos{70^{\circ}}\right]\cdot\sin{20^{\circ}}\cdot\sin{80^{\circ}}=\sin\left(\angle{BDA}\right)\cdot\dfrac{\sqrt{3}}{4}$
$\sin{20^{\circ}}\cdot\sin{70^{\circ}}\cdot\sin{80^{\circ}}\cdot cos\left(\angle{BDA}\right)=\sin\left(\angle{BDA}\right)\left[\dfrac{\sqrt{3}}{4}+\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}\right]$
$\tan\left(\angle{BDA}\right)=\dfrac{\sin{20^{\circ}}\cdot\sin{70^{\circ}}\cdot\sin{80^{\circ}}}{\dfrac{\sqrt{3}}{4}+\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}$
This last equation can be simplified to:
$\tan\left(\angle{BDA}\right)=\dfrac{1}{\sqrt{3}}$
$\therefore\angle{BDA}=30^{\circ}$
This is the answer.
For the sake of clarity, the (long) simplification follows:
$\dfrac{\sin{20^{\circ}}\cdot\sin{70^{\circ}}\cdot\sin{80^{\circ}}}{\dfrac{\sqrt{3}}{4}+\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}=\dfrac{4\cdot\sin{20^{\circ}}\cdot\sin{70^{\circ}}\cdot\sin{80^{\circ}}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}$
The product $\left(\sin{20^{\circ}}\cdot\sin{70^{\circ}}\right)$ may be represented as the difference of cosines, such that
$\cos{90^{\circ}}-\cos{50^{\circ}}=-2\cdot\sin{\dfrac{90^{\circ}+50^{\circ}}{2}}\cdot\sin{\dfrac{90^{\circ}-50^{\circ}}{2}}$
$0-\cos{50^{\circ}}=-2\cdot\sin{70^{\circ}}\cdot\sin{20^{\circ}}$
$\cos{50^{\circ}}=2\cdot\sin{70^{\circ}}\cdot\sin{20^{\circ}}$
Continue,
$\dfrac{4\cdot\sin{20^{\circ}}\cdot\sin{70^{\circ}}\cdot\sin{80^{\circ}}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}=\dfrac{2\cdot\cos{50^{\circ}}\cdot\sin{80^{\circ}}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}$
The product $\left(2\cdot\sin{80^{\circ}}\cdot\cos{50^{\circ}}\right)$ may be represented as the sum of sines, such that
$\sin{130^{\circ}}+\sin{30^{\circ}}=2\cdot\sin{\dfrac{130^{\circ}+30^{\circ}}{2}}\cdot\cos{\dfrac{130^{\circ}-30^{\circ}}{2}}$
$\sin{\left(90^{\circ}+40^{\circ}\right)}+\dfrac{1}{2}=2\cdot\sin{80^{\circ}}\cdot\cos{50^{\circ}}$
$\cos{40^{\circ}}+\dfrac{1}{2}=2\cdot\sin{80^{\circ}}\cdot\cos{50^{\circ}}$
since $\cos{40^{\circ}}=\sin{50^{\circ}}$
$\sin{50^{\circ}}+\dfrac{1}{2}=2\cdot\sin{80^{\circ}}\cdot\cos{50^{\circ}}$
Continue,
$\dfrac{2\cdot\cos{50^{\circ}}\cdot\sin{80^{\circ}}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}$
The product $\left(2\cdot\sin{20^{\circ}}\cdot\sin{80^{\circ}}\right)$ may be represented as the difference of cosines, such that
$\cos{100^{\circ}}-\cos{60^{\circ}}=-2\cdot\sin{\dfrac{100^{\circ}+60^{\circ}}{2}}\cdot\sin{\dfrac{100^{\circ}-60^{\circ}}{2}}$
$\cos{\left(90^{\circ}+10^{\circ}\right)}-\dfrac{1}{2}=-2\cdot\sin{80^{\circ}}\cdot\sin{20^{\circ}}$
$-\sin{10^{\circ}}-\dfrac{1}{2}=-2\cdot\sin{80^{\circ}}\cdot\sin{20^{\circ}}$
$\sin{10^{\circ}}+\dfrac{1}{2}=2\cdot\sin{80^{\circ}}\cdot\sin{20^{\circ}}$
Continue,
$\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+4\cdot\left(\sin{20^{\circ}}\right)^{2}\cdot\sin{80^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+2\cdot\sin{20^{\circ}}\cdot\left(\sin{10^{\circ}}+\dfrac{1}{2}\right)}$
$=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+2\cdot\sin{20^{\circ}}\cdot\sin{10^{\circ}}+\sin{20^{\circ}}}$
The product $\left(2\cdot\sin{20^{\circ}}\cdot\sin{10^{\circ}}\right)$ may be represented as the difference of cosines, such that
$\cos{30^{\circ}}-\cos{10^{\circ}}=-2\cdot\sin{\dfrac{30^{\circ}+10^{\circ}}{2}}\cdot\sin{\dfrac{30^{\circ}-10^{\circ}}{2}}$
$\dfrac{\sqrt{3}}{2}-\cos{10^{\circ}}=-2\cdot\sin{20^{\circ}}\cdot\sin{10^{\circ}}$
$2\cdot\sin{20^{\circ}}\cdot\sin{10^{\circ}}=\cos{10^{\circ}}-\dfrac{\sqrt{3}}{2}$
Continue,
$\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+2\cdot\sin{20^{\circ}}\cdot\sin{10^{\circ}}+\sin{20^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}+\cos{10^{\circ}}-\dfrac{\sqrt{3}}{2}+\sin{20^{\circ}}}$
$=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}+\sin{80^{\circ}}+\sin{20^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}+\left(2\cdot\sin{\dfrac{80^{\circ}+20^{\circ}}{2}}\cdot\cos{\dfrac{80^{\circ}-20^{\circ}}{2}}\right)}$
$=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}+2\cdot\sin{50^{\circ}}\cdot\cos{30^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}+\sqrt{3}\cdot\sin{50^{\circ}}}=\dfrac{\sin{50^{\circ}}+\dfrac{1}{2}}{\sqrt{3}\left(\dfrac{1}{2}+\sin{50^{\circ}}\right)}$
$=\dfrac{1}{\sqrt{3}}$