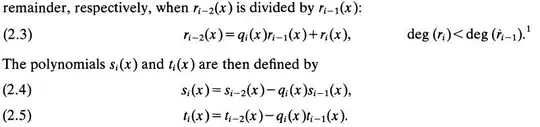4

I'm not sure if this question is entirely on-topic here, please notify if not. I feel it is more a math related problem, than a programming problem.

Following the advice in this answer I'm trying to implement the Extended Euclidean Algorithm. The linked answer as well as one of the standard sources:

McEliece, Robert J.; Shearer, James B., A property of Euclid’s algorithm and an application to Padé approximation, SIAM J. Appl. Math. 34, 611-615 (1978). ZBL0384.10006.

yield the same results, when I implement them. However, my results do not match the example given in McEliece and I have a hard time figuring out what I'm doing wrong.

The example given is: enter image description here enter image description here enter image description here

My Code: using Matlab's quorem function:

syms a b x r t q s

a = x^7;
b = -x^6 + x^5 - x^3 + x^2 + x + 1;

s(-1+2) = 1;
t(-1+2) = 0;
r(-1+2) = a;
s(0+2) = 0;
t(0+2) = 1;
r(0+2) = b;

for k = 1:4
    [q(k+2), r(k+2)] = quorem(r(k-2+2),r(k-1+2),x);
    s(k+2) = s(k-2+2) - q(k+2)*s(k-1+2);
    t(k+2) = t(k-2+2) - q(k+2)*t(k-1+2);
end

disp( [ (1:5).'-2 r(:), q(:) ] )

(the +2 just shifts the index to a valid range)

yields to for $r_i$ and $q_i$:

[ -1,                             x^7,              q]
[  0, - x^6 + x^5 - x^3 + x^2 + x + 1,              0]
[  1,     x^5 - x^4 + 2*x^2 + 2*x + 1,        - x - 1]
[  2,           x^3 + 3*x^2 + 2*x + 1,             -x]
[  3,             - 21*x^2 - 14*x - 9, x^2 - 4*x + 10]
[  4,                            x/63,   - x/21 - 1/9]
[  5,                               0,              0]

Which is similar, but starting with line 3, not the same. I checked the code a dozen times, what am I doing wrong?

hardmath
  • 37,715
Robert Seifert
  • 285
  • 1
    You are aware that the paper computes in the finite field $\Bbb F_3$, that is, all coefficients are modulo $3$? – Lutz Lehmann Jan 25 '18 at 15:51
  • @LutzL To be honest, I don't even understand what that means. As it does not reappear in the paper, and you haven't mentioned anything like that in your last answer, I just overread it. How does this phrase alter my results? – Robert Seifert Jan 25 '18 at 16:02
  • 1
    You get $21\mod 3 = 0$, $14 \mod 3 = -1$ etc. The computation in remainder classes can have a different degree path in the remainders depending on the prime that is used for the finite field/Galois field. In other words, your algorithm gives the correct result if the ground field for the polynomial ring is the rational numbers. – Lutz Lehmann Jan 25 '18 at 16:51
  • 1
    @LutzL I know what modulo means, but the rest of your comment sounds like a sealed book to me. But I learned, that my implementation may is not wrong, I just need an example for rational numbers. – Robert Seifert Jan 25 '18 at 21:02
  • @LutzL do you mind if I answer my own question, or do you want to write something? I got a working case for rational numbers now. – Robert Seifert Jan 26 '18 at 09:07
  • 1
    I've assembled my comments into an answer. If you want to present improved matlab code as answer, go ahead, I have no matlab present to test code. For the overarching problem of computing Padé approximants, the finite field computations are not relevant. They were used in the paper as they keep the coefficients small during the computation, which is in general not the case for the polynomial Euclidean algorithm. See subresultant algorithm for a method to control the coefficient growth somewhat.. – Lutz Lehmann Jan 26 '18 at 09:53
  • @LutzL thanks a lot, I added corrected code! – Robert Seifert Jan 26 '18 at 10:34

2 Answers2

2

You did everything right except to understand the first sentence in the example:

Let $\Bbb F_3=\{-1,0,1\}$ be the field of integers modulo $3$ ...

This means that all integer computations are reduced to these numbers by adding or subtracting multiples of $3$. So that you get $1+1=-1$, as $2=-1+3$. In this sense,

  • the computed $r_2=x^3 + 3*x^2 + 2*x + 1$ is then reduced to $x^3 + 0*x^2 - x + 1$ and
  • in the next step, $r_3=- 21*x^2 - 14*x - 9$ gets reduced to $0*x^2+x-0$.

As the reduction to coefficients in $\Bbb F_3$ changes the degree of $r_3$, all the following computations have to be more different than just changes by multiples of $3$. This can be seen for instance in the next remainder where the division $r_4=x/63$ is a division by zero in $\Bbb F_3$.

Lutz Lehmann
  • 131,652
2

In addition to the explaining answer of LutzL, here the corrected Matlab code, compared with Matlab's in-built function:

% Variable declaration:
syms a b x r t q s

% Example:
m = 4;
n = 3;
% Taylor expansion with minimum order of m+n
b = x^7 -x^6 + x^5 - x^3 + x^2 + x + 1;
% =>
a = x^(m+n+1);

% starting values
s(-1+2) = 1;
t(-1+2) = 0;
r(-1+2) = a;
s(0+2) = 0;
t(0+2) = 1;
r(0+2) = b;

% algortihm
poldeg = @(pol) feval(symengine, 'degree', pol, x);
k = 1;
while true
    [q(k+2), r(k+2)] = quorem(r(k-2+2),r(k-1+2),x);
    s(k+2) = s(k-2+2) - q(k+2)*s(k-1+2);
    t(k+2) = t(k-2+2) - q(k+2)*t(k-1+2);
    if poldeg(r(k)) == m; break; end
    k = k+1;
end

% Pade Approximant by Extended Euclidan Algorithm
PA = simplifyFraction(r(k)/t(k))

% Check with in-built function:
PA = pade(b,x,0,'Order',[m,n])

PA (this implementation) = (x^3 + 3*x^2 + 2*x + 1)/(x^2 + x + 1)
PA (Matlab in-built) = (x^3 + 3*x^2 + 2*x + 1)/(x^2 + x + 1)
Robert Seifert
  • 285