Given the following function: $$f(t)=\sin(\omega_0 t+\phi_0(t))$$ with: $$\phi_0(t)=\sin(\omega_1t+\phi_1(t))$$ $$\phi_1(t)=\sin(\omega_2t+\phi_2(t))$$ $$\phi_k(t)=\sin(\omega_{k+1}t+\phi_{k+1}(t))$$ $$\phi_N(t)=\sin(\omega_{N+1}t+\phi_{N+1})$$ Under what conditions the $f(t)$ can be periodic? Thanks.
-
What is the relationship between $\omega_k$? If they are all the same, the function is periodic. For other cases I don't know – Yuriy S Jan 23 '18 at 16:24
-
Somewhat related: http://math.stackexchange.com/questions/1652612/smooth-sawtooth-wave-yx-cosx-cosx-cosx-dots – Yuriy S Jan 23 '18 at 16:27
-
@YuriyS: the case $\omega_k$ all the same is the trivial case. There is'nt any relation between the $\omega$ – Riccardo.Alestra Jan 23 '18 at 16:36
1 Answers
Some simple considerations. Leaving the question of convergence aside.
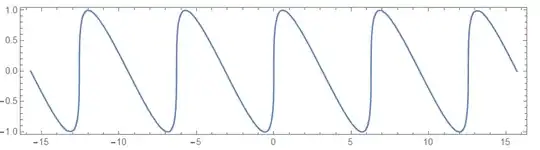
Start from the so-called 'trivial case' of $\omega_k=\omega_0$ for all $k$. It's obviously periodic, since at each recursive step the functions are periodic with the same period. The plot looks like this:
Now for the more general case:
$$\omega_{k+p}=\omega_k, \qquad p \in \mathbb{N}$$
In this case $\omega_p=\omega_0$ and the rest:
$$\omega_{j}=q_j \omega_0, \qquad j \in [1,p-1]$$
I conjecture that for $q_j \in \mathbb{Q}$, i.e. rational, and for any finite $p$ the function is periodic.
It can be concluded from the usual trigonometric formulas for angle transformation, since they all involve rational multiples of the original angle/frequency.
Another conjecture is that if at least one $q_j$ is irrational then the resulting function is not periodic.
In principle $p$ can be infinite, but only if all $q_j$ are known and their denominators are bounded (see below).
Some examples:
$$p=2, \qquad \omega_1=2 \omega_0$$
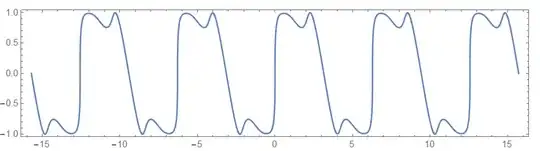
$$p=3, \qquad \omega_1=3 \omega_0, \qquad \omega_2=2 \omega_0$$
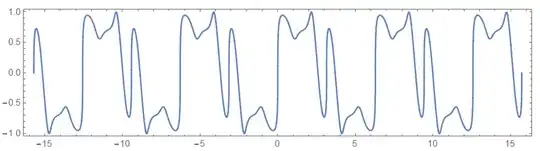
$$p=2, \qquad \omega_1=\frac{3}{7} \omega_0$$
The period of the function becomes larger for $q_j$ not an integer because the original period related to $\omega_0$ has to be multiplied by the denominator.
- 32,728