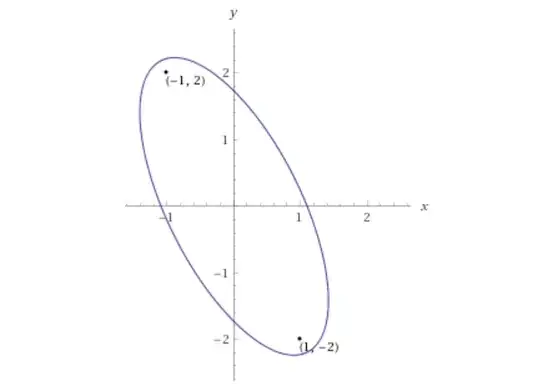
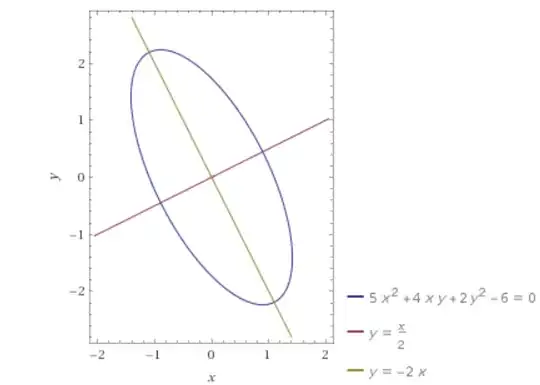
Which points on the curve $5x^2+4xy+2y^2-6=0$ are closest to the origin.

Question

Which points on the curve $5x^2+4xy+2y^2-6=0$ are closest to the origin.

I have solved countless of problems like this but this one is just giving me such a hard time. I'm supposed to solve this with Lagrange's method. So I want to minimize $f(x,y)=x^2+y^2$ due to the constraint $g(x,y)=5x^2+4xy+2y^2-6=0$.

Ok easy: Find $x,y$ so the following equations are satisfied:

$2x+\lambda(10x+4y)=0$

$2y+\lambda(4y+4x)=0$

$5x^2+4xy+2y^2-6=0$

Right? But however i do, i get very complicated equations with root terms to solve, getting me nowhere. I would love to see how you would solve this. Thanks.

Answer 1

We have: $$2x +10\lambda x +4\lambda y =0 \tag 1$$ $$2y +4\lambda x + 4\lambda y =0 \tag 2$$ Now, $x(1)+y(2)$ gives us after simplification: $$x^2+y^2=-6\lambda \tag 3$$

Solving for $x$ and $y$ from $(1)$ and $(2)$ gives us: $$x =-\frac{2\lambda y} {1+5\lambda}$$ $$y =-\frac{2\lambda x} {1+2\lambda}$$

Solving for $\lambda$ gives us the equation: $$(6\lambda +1)(\lambda +1)=0$$

Then conclude $(3)$ using an appropriate $\lambda$

Answer 2

If Lagrange multiplier is not mandatory,

using rotation of axes,

$$X=x\cos t+y\sin t,Y=-x\sin t+y\cos t$$

If the new equation of the given curve is $$A'X^2+B'Y^2+F'=0$$

$$\cot2t=\dfrac{2-5}4=-\dfrac34$$ $$\iff\dfrac{\cos 2t}{-3}=\dfrac{\sin2t}4=\pm\dfrac15$$

If $\cos2t=-\dfrac35,\sin2t=\dfrac45$

$$2A'=5(1+\cos2t)+4\sin2t+2(1-\cos2t)=?$$

$$2C'=A'(1-\cos2t)-4\sin2t+2(1+\cos2t)=?$$

$$F'=6$$

So, any point on the ellipse can be $$\sqrt{\dfrac 6{A'}}\cos u,\sqrt{\dfrac 6{C'}}\sin u$$

As the origin is invariant under rotation, we need to minimize $$\dfrac{6\cos^2u}{A'}+\dfrac{6\sin^2u}{C'}$$

Answer 3

With the help of modern tools like Wolfram Alpha, one can visualize and identify as an ellipse the curve described by $$5x^2+4xy+2y^2-6=0.$$ Also the foci can be determined as shown below:

It turns out (join the foci) that the equations of the lines of the great and the small axes are $$y=-2x\text{ and } y=\frac12x$$:

The nearest points (to the origin) are at the intersection points of $y=\frac12x$, the line of the small axis, and the ellipse. So, let's substitute $\frac12x$ in to $5x^2+4xy+2y^2-6=0$. We get $5x^2+x^2+\frac12x^2=6$ or or $x=\pm\sqrt{\frac6{13}}$. To find $y$ is easy now.

Answer 4

Let $x^2+y^2=k$.

Thus, we need to find all points $(x,y)$ such that $$5x^2+4xy+2y^2=6$$ for which $k$ gets a minimal value, which says the equation $$x^2+y^2=k\cdot\frac{5x^2+4xy+2y^2}{6}$$ has solutions or $$(5k-6)x^2+4kxy+(2k-6)y^2=0,$$ which for $k\neq\frac{6}{5}$ gives $$4k^2-(5k-6)(2k-6)\geq0$$ or $$k^2-7k+6\leq0,$$ which gives $$1\leq k\leq6.$$ Since $1<\frac{6}{5}$, we see that $1$ is a minimal value of $k$ because the equality occurs for $$-x^2+4xy-4y^2=0,$$ which gives $x=2y$ and we got two following points:

$\left(\frac{2}{\sqrt5},\frac{1}{\sqrt5}\right)$ and $\left(-\frac{2}{\sqrt5},-\frac{1}{\sqrt5}\right)$

Answer 5

Function and constraint are

$$ F = 5 x^2+ 4 xy + 2 y^2 -6 =0,\, G= x^2+y^2 -1=0 $$

as usual to find LM

$$ \frac{F_x}{F_y} = \frac{G_x}{G_y} ;\, \frac{10x +4y}{4x+4y} = \frac{x}{y} $$ cross multiply, simplify, solve for $y/x$

$$ 2y^2 +(3/2) x y - 2 y^2 =0 \rightarrow y= x/2,\, y= -2 x $$

These directions (slope $=\dfrac12, -2) $ are indicated below for arbitrary variation of those constants in Mathematica plot:

No matter what the stand alone constants $(1,6)$ are.. these directions are the same. Particular points of intersection can be found, and that means a particular Lagrange Multiplier choice, by plug-in of these lines to find intersection of line/ellipse.