Elementary proof of transformations of domino tilings.

Question

There is a theorem that says you can transform one tiling by dominoes of a figure without holes to another by a sequence of flips (rotating pairs of dominoes that share a long edge.) The usual proof (see for example this question) uses "height functions" and some algebra; I am trying to construct a proof without using those tools, and I am nearly there.

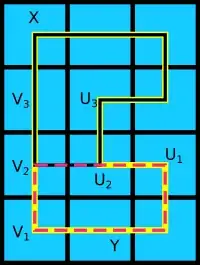
The last bit that remains is to prove that every closed path of cells without holes on a square lattice has four consecutive cells that form a square, called a knob. This seems very obvious, but I cannot come up with a proof of this fact.

In this figure, there are two knobs (marked yellow and pink).

My question is: how can I prove every path without holes has a knob?

---

Edit: My original idea was to use the idea of a knob to get a way to do induction on certain types of paths. However, the proof we came up with is itself an induction proof, and I could use the method directly instead of needing to use knobs. I also discovered a few problems with my original proof plan (although the overall strategy stayed in tack. I removed some of the details I had here originally (mostly because they are wrong and not very insightful otherwise).

---

To see how this fits into my proof, here is a sketch.

A strip polyomino is a polyomino whose cells form a path. A closed strip is a strip polyomino whose cells form a closed path. A closed strip has at least two tilings ($\{c_1, c_2\}, \{c_3, c_4\}$, etc. and $\{c_n, c_1\}, \{c_2, c_3\}$, etc.).

If we have a tiled figure, and a subfigure which is a tiled closed strip, then replacing the closed strip's tiling with the dual tiling is called a strip rotation. (A flip is a special case of a strip rotation).

1. We can get one tiling of any figure from another by strip rotations. Pick any cell $c_1$ covered by dominoes in different ways in the two tilings, and construct a closed strip by picking a neighbor $c_2$ in the same domino in the one tiling, then a neighbor $c_3$ of $c_2$ within the same domino in the other tiling, etc. This must end when the next neighbor is $c_1$. (It's always possible to pick a next cell, and we can never pick a next cell again before picking $c_1$, and the figure is finite.)

Now performing a strip rotation on this strip makes all the tiles match the second tiling. We repeat the process until the transformed tiling matches the second tiling completely. (Notice that in constructing the strip we never pick patches where dominoes in the two tilings match, so we will never "undo" dominoes already in place.)

2. A strip rotation of a strip without holes is equivalent to a sequence of flips. This is the part that requires induction. The idea is to show it for paths that correspond to a flip (rotating two dominoes) as the base case, and then to show that a path always contains a smaller path, and that with a flip of the rest and a rotation on the smaller path, we get a rotation on the bigger path. (There are a few cases here to consider.)

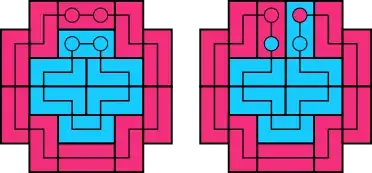
3. A strip rotation of a closed strip with a filled interior is equivalent to a series of flips. The idea here is to inductively add dominoes of the path's interior to the path, at times doing flips, and at times shedding dominoes from the path, until we are left with a bunch of paths that correspond to strip polyominoes without holes.

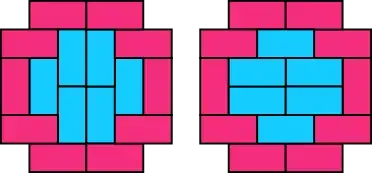
Here is a simple example:

We then perform strip rotations on some of these (some may already be "in position"), which we already proved is equivalent to flips, to get the original path rotated, but potentially part of its interior too. We then rotate the interior (or each path thereof), so that the interior is back the way it started. We are left with only the outer path rotated.

By combining 1 and 3, we arrive at the result: One tiling of a figure without holes can be transformed to another with a sequence of flips.

Answer 1

Edit: With additional ideas from Colm Bhandal (see comments) the proof is now shorter (and clearer) than the original version. He also mentions implicit reliance on the Jordan Curve theorem. I am not so confident about how that fits into the proof; perhaps somebody can edit it in.

The trick is to use a different definition of a knob, and then prove that every path that corresponds to a closed strip without holes have at least two knobs.

---

Let a knob be three edges of a unit square. Knobs can overlap, but when they do the path must be a square.

We prove that every closed non-self-intersecting path that corresponds to a closed strip polyomino without holes must have at least two knobs using induction.

It is clearly true for the smallest such path (a unit square), which has in fact 4 knobs.

Suppose it is true for all such paths of length $n$ or smaller. Consider a path of length $n + 2$. (Note that path length must be even if the path is closed.)

Find a left-most long-edge of length 2 or higher. (Using the idea at the beginning of Colm Bhandal's proof. If we cannot, we rotate the path 180 and find a long edge and proceed. If we cannot yet again, we have two knobs and we are done.)

Let the vertices of the path be $P = V_1$, $V_2$ and $V_3$.

Now one unit to the right of $V_2$, we must have another vertex. (If we did not, there would be a hole in the corresponding strip polyomino.)

Let this vertex be $U_2$, and its two neighbors $U_1$ and $U_3$. So if the original path was $V_1, V_2, V_3, X_1, X_2, X_3..., U_3, U_2, U_1, Y_1, Y_2, Y_3, ... [V_1]$ we can make two paths $P_1 = V_1, V_2, U_2, U_1, Y_1, Y_2, Y_3, ..., [V_1]$ and $P_2 = V_3, V_2, U_2, U_3, ... X_3, X_2, X_1, [V_3]$.

We now want to apply the inductive hypothesis to both of our paths. Before doing so, we simply need to prove some conditions about theses child paths:

1. Both paths are closed- this is immediate from their definition in which the start vertex matches the end vertex.
2. Both paths are non-self-intersecting. For a "digital path" like this, we know it's non-self intersecting whenever there are at most two edges adjacent to each node in the path. Indeed, since we only added one edge $v_2u_2$, we must only check the nodes $v_2$ and $u_2$ for this condition. Clearly, at each of these two vertices, the new edge has been added but an old edge has been removed, in each path. So this condition is satisfied.
3. Both paths contain no holes. We employ the Jordan Curve Theorem for this. The closed, non-self-intersecting nature of the "mother path" means it has an interior and an exterior. Because we started off by choosing the leftmost strip, we know that the region to the left of it cannot possible be the interior of the path, else there'd have to be nodes further to the left. This means the region immediately to the right of it is in the interior. The same argument can be applied to the two "children" paths. Now, here is the key point. Each child path's interior can be regarded as the set of points in the mother path minus the set of points in the other child path. We want to prove that this set subtraction does not create any holes. Well, let's say it did, towards a contradiction. Then the interior of one path would exist within the interior of the other. But, by the very definition of interior, then any point in the interior of one path could be reached via some curve, without intersecting any edges, from the interior of the other. In other words, both paths would have to share the exact same interior, meaning they would be the same path. This is clearly not the case, so we can happily conclude the paths are hole-free.
4. Both paths must have length $n$ at most. Well, this is obvious because one path is missing at least two edges from the mother path: $v_1v_2$ and $u_1u_2$. The other path is missing at least $v_2v_3$ and $u_2u_3$. So both paths have at most $n$ edges.

Thus, by induction, both new paths must have at least two knobs each. Now, in each of these paths, we count how many of the knobs can contain the newly added edge $v_2u_2$:

• Well, in the lower path, the only knob that this edge can belong to is $Y, v_1, v_2$, where I abuse the $Y$ notation here to mean the last node in the $Y$ sequence.
• In the upper path, the only knob our new edge can belong to is $u_3, u_2, v_2, v_3$.

So, in both cases, there is at least one knob left over from the original path. Since both child paths are disjoint, this implies that there are at least two knobs in the mother path.

Answer 2

PROOF INCORRECT - SEE COMMENTS

We can prove the existence of a knob in a closed path with no holes as follows. Imagine a bounding rectangle around the path. This implies a leftmost $x$ coordinate.

Now go to any tile on the path with this $x$ value. Now, trivially, it will be in a vertical run of $1$ or more tiles, but on closer inspection we know there must be at least $2$ tiles in the vertical run, because the path only has $3$ directions to choose from, this being the leftmost tile, and because the path has backwards and forwards direction, $2$ out the $3$ possible adjacent tiles must be in the path, one of which must be vertical by something like the pigeonhole principle.

At the top and bottom of this vertical run, it must curve to the right, giving a shape like the open square bracket: [, as shown in the image below.

Now, let's call $m$ the number of tiles in the run. At best, $m = 2$, and we have a knob, and we're done. Else, go to the next column to the right.

In this column, between the top and bottom parts of our square bracket, all the cells must be filled in (this is where the proof breaks down, see below), because the path cannot contain a hole. But there are exactly $m-2 < m$ cells here, so any vertical run contained in here must $r$ cells with $r \leq m - 2 < m$.

Now, let's say at either the top or the bottom of our run of $r$ cells, the path continued on straight. Then we'd have a knob, joining on to one or the other of the little parts of the original square bracket shape. (See the image below for this situation.) We also know the run can't curve left, because the original run can't be intersected. So the run must form another square bracket shape curving to the right.

Thus we can show by infinite descent that either a knob occurs or $m$ reaches the value $2$, in which case a knob is forced.

Counterexample

Unfortunately the proof breaks down because the cells inside the square bracket need not in fact be filled in. Here is an example that shows this situation.