$$\sum_{r = 0}^{n^2} (-1)^r \binom{n^2+n}{r}$$
This is what Wolfram says:
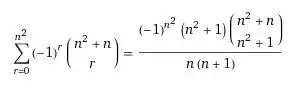
Is there any simple way to prove it? Like with counting arguments or manipulating binomial expansions?
$$\sum_{r = 0}^{n^2} (-1)^r \binom{n^2+n}{r}$$
This is what Wolfram says:
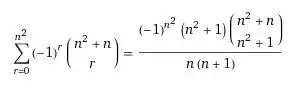
Is there any simple way to prove it? Like with counting arguments or manipulating binomial expansions?
Using Vandermonde's Identity: $$ \begin{align} \sum_{r=0}^{n^2}(-1)^r\binom{n^2+n}{r} &=\sum_{r=0}^{n^2}(-1)^{n^2}\binom{n^2+n}{r}\binom{-1}{n^2-r}\\ &=(-1)^{n^2}\binom{n^2+n-1}{n^2} \end{align} $$
This is a case of $$\sum_{r=0}^k(-1)^r\binom mr=(-1)^k\binom{m-1}k$$ which is easily proved by induction on $k$.
$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} \color{#44f}{\sum_{r = 0}^{n^{2}}\pars{-1}^{r}{n^{2} + n \choose r}} & = \sum_{r = 0}^{n^{2}}\pars{-1}^{r}{n^{2} + n \choose n^{2} + n - r} \\[5mm] & = \sum_{r = 0}^{n^{2}}\pars{-1}^{r} \bracks{z^{n^{2}\ +\ n\ -\ r}\,\,} \pars{1 + z}^{n^{2}\ +\ n} \\[5mm] & = \bracks{z^{n^{2}\ +\ n}}\pars{1 + z}^{n^{2} + n}\sum_{r = 0}^{n^{2}}\pars{-z}^{r} \\[5mm] & = \bracks{z^{n^{2} + n}}\pars{1 + z}^{n^{2} + n} \,{\pars{-z}^{n^{2} + 1} - 1 \over -z - 1} \\[5mm] & = \bracks{z^{n^{2}\ +\ n}}\pars{1 + z}^{n^{2} + n - 1} + \pars{-1}^{n^{2}}\ \times \\ & \phantom{=\,\,\,}\bracks{z^{n - 1}} \pars{1 + z}^{n^{2} + n - 1} \\[5mm] & =\ \underbrace{{n^{2} + n - 1 \choose n^{2} + n}}_{\ds{=\ 0}}\ +\ \pars{-1}^{n^{2}}{n^{2} + n - 1 \choose n - 1} \\[5mm] & = \bbx{\color{#44f}{\pars{-1}^{n^{2}}{n^{2} + n - 1 \choose n - 1}}} \\ & \end{align}