5

Below is the definition of foliation of a manifold appearing in the book Introduction to Foliations and Lie Groupoids by Moerdijk and Mrčun.

Definition 1. Let $M$ be a smooth manifold of dimension $n$. A foliation atlas of codimension $m$ of $M$ is an atlas $$(\varphi_i:U_i\to \mathbb R^n\cong \mathbb R^{n-m}\times \mathbb R^m)_i$$ of $M$ for which the change-of-charts diffeomorphisms $\varphi_{ij}$ are locally of the form $$\varphi_{ij}(x,y)=(g_{ij}(x,y),h_{ij}(y))$$ with respect to the decomposition $\mathbb R^n\cong \mathbb R^{n-m}\times \mathbb R^m$.

I am confused by this definition.

Question 1. I don't understand why $h_{ij}$ need not be the identity - don't we want the hyperplane at height $y$ to map into itself?

  1. In the book Geometric Theory of Foliations by Camacho and Neto, §1 begins by considering the usual submersion $\mathbb R^n\to \mathbb R^m$ and then writing:

The diffeomorphisms [...] which preserve the leaves of this foliation locally have the following form $$\varphi_{ij}(x,y)=(g_{ij}(x,y),h_{ij}(y)).$$

However Figure 1 seems to suppose $\varphi_{ij}$ does map the horizontal line at height $y$ into itself, which would make $h_{ij}$ the identity.

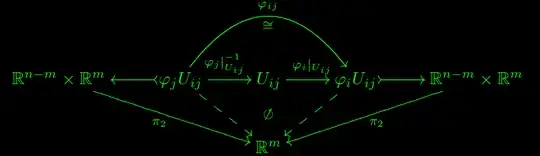
  1. From a formal perspective, the reasonable condition to ask seems to be the commutativity of the triangle with broken sides below, where the broken arrows are defined by composites of the obtuse triangles.

enter image description here

Using the universal property of the product commutativity then implies $\varphi_{ij}=(g_{ij},\pi_2|_{\varphi_iU_{ij}})$, making $h_{ij}$ the identity as expected.

Let $(U_i)$ be an open cover of $M$ and consider a family of bundles $(\begin{smallmatrix}L_i\\ \downarrow\\ U_i\end{smallmatrix})$. Recall that descent data for the family $(\begin{smallmatrix}L_i\\ \downarrow\\ U_i\end{smallmatrix})$ consists of transition isomorphisms $\varphi_{ij}:\begin{smallmatrix}L_j\\ \downarrow\\ U_j\end{smallmatrix}|_{U_{ij}}\cong \begin{smallmatrix}L_i\\ \downarrow\\ U_i\end{smallmatrix}|_{U_{ij}}$ satisfying the cocycle condition.

Recall also the existence of a bundle over $M$ pulling back to the family $(\begin{smallmatrix}L_i\\ \downarrow\\ U_i\end{smallmatrix})$ is equivalent (at least in the topological case) to the existence of descent data for this family.

It seems the above definition of foliation is very closely related to the specification of descent data. Moreover, a foliation can be viewed as a smooth bijection $L\to M$ from the leaf manifold, and I feel the leaf manifold should perhaps by obtained using the usual gluing construction of bundles using descent data.

Question 2. What is the descent data and the family of bundles here and how do they give rise to the smooth bijection from the leaf manifold $L\to M$?

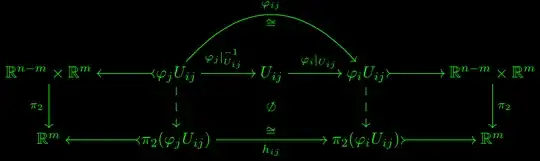
Added. Following Eric Wofsey's answer, here's the correct diagram (generally not commutative).

enter image description here

Arrow
  • 14,390
  • What do you mean by "the leaf manifold"? The disjoint union of the leaves? – Eric Wofsey Dec 31 '17 at 23:28
  • I was referring to the first definition of foliation in Milnor's Foliations and foliated vector bundles. I think I made an error though, since the $L$ in Milnor's notes is in bijection with $M$, while the leaf space is generally different e.g for a submersion it is the space of the connected components of its fibers. – Arrow Jan 01 '18 at 00:56

2 Answers2

4

No, the hyperplane of height $y$ does not need to map to itself. There is no well-defined hyperplane of height $y$. The collection of all the hyperplanes is locally well-defined (the hyperplane of height $y$ must be sent to some other hyperplane, namely that of height $h_{ij}(y)$) but the height of any particular hyperplane is not.

As for your second question, you can define the local leaf space $L_i$ over $U_i$ to just be the disjoint union of the hyperplanes which make up your chart over $U_i$ (in other words, $L_i$ is an open subset of $\mathbb{R}^{n-m}\times\mathbb{R}^m_d$ where the $d$ indicates you are considering $\mathbb{R}^m$ as a discrete, $0$-dimensional manifold). The total leaf space is then obtained by gluing together all these local leaf spaces via the $\varphi_{ij}$. The condition that the second coordinate of $\varphi_{ij}$ has the form $h_{ij}(y)$ (that is, it doesn't depend on $x$) exactly guarantees that the $\varphi_{ij}$ are still diffeomorphisms even when you deal with $\mathbb{R}^{n-m}\times\mathbb{R}^m_d$ instead of $\mathbb{R}^{n}$.

Eric Wofsey
  • 342,377
  • Thanks as always. Regarding the diagram - if the bottom vertex $\mathbb R^m$ were expanded into a diffeomorphism $h_{ij}$ of $\mathbb R^m$, and we asked the resulting square with broken sides to commute, then that would retrieve the definition, right? – Arrow Jan 01 '18 at 00:30
  • Well, that's correct up to the issue that the diffeomorphism $h_{ij}$ may only be locally defined. That is, it's a diffeomorphism between two open subsets of $\mathbb{R}^m$, not necessarily from all of $\mathbb{R}^m$ to all of $\mathbb{R}^m$. – Eric Wofsey Jan 01 '18 at 00:33
  • Right. Thanks for catching that. So $h_{ij}$ need only be defined between $\pi_2(\varphi_j(U_{ij}))$ and $\pi_2(\varphi_i(U_{ij}))$. – Arrow Jan 01 '18 at 00:34
1

It is not that complicated, you can identify $U_i$ with an open subset of $\mathbb{R}^n$ on $U_i$ the leaves of the restriction of the foliation are defined by $y=c$ where $c$ is a constant, they are the intersection of the affine space $y=c$ with $U_i$, the fact that the coordinate change have the $(g_{ij}(x,y),h_{ij}(y))$ implies that they preserves the restriction of the foliation to $U_i\cap U_j$ since the image of $y=c$ is sent to $h_{ij}(y)=c$ by the coordinate change, so you can glue the foliation defined on $U_i$ to define a foliation $M$.

Tsemo Aristide
  • 89,587