5

For me a rational map $X \to Y$ is a morphism defined on a dense open set of $X$, with the equivalence relation that $f: U \to Y \ \ \sim \ \ g: V \to Y$ if there is a dense open set $Z \subset U \cap V$ such that $f|_Z = g|_Z$, and $X$ and $Y$ are birational if there are dominant rational maps $f: X \to Y$ and $g: Y \to X$ such that $f \circ g$ and $g \circ f$ are both identity (up to the previous equivalence relation). This is the definitions given in section 6.5 of Vakil.

I found an answer to my question here, but I don't see how the definition they used is the same as mine. i.e., why a rational map $X \to Y \subset \mathbb{P}_k^N$, where $X$ and $Y$ are smooth projective curves, can be written as $x \mapsto [f_1(x):...:f_N(x)]$ where $f_i \in k(x)$.

If anyone can give me a different proof of the question, that would be nice too.

Thanks!

reuns
  • 79,880
Aaron Johnson
  • 1,096
  • Embedding $X,Y$ in $\mathbb{P}^N$ means there are two homogeneous ideals $I,J \subset k[x_0,\ldots,x_N]$ such that $X = { x = [x_0:\ldots:x_N] \in \mathbb{P}^N, \forall h \in I, h(x_0,\ldots,x_N) = 0}$ and $Y = { y \in \mathbb{P}^N,\forall g \in J, g(y) = 0}$.

    Then a rational map $U \subset X \to \mathbb{P}^N$ will be of the form $x \mapsto [f_0(x):\ldots :f_N(x)]$ with $f_j \in k(x_0,\ldots,x_N)$

     – reuns Dec 26 '17 at 06:29
  • I understand what embedding into $\mathbb{P}_k^N$ means, but how does that relate to your last sentence? Do you define $x \mapsto [f_0(x):...f_N(x)]$ for all $x$ in $X$? It seems like that's what they did in the post I linked to, but using my definition we don't have a map outside an open dense set. Sorry if this is silly, I don't have much experience with classical algebraic geometry. – Aaron Johnson Dec 26 '17 at 07:03
  • The $f_j$ are quotient of polynomials $\in k[x_0,\ldots,x_n]$ so $f_j(x), x \in k^{n+1}$ is well-defined only if the denominator is non-zero. Considering only polynomials $\in k[x_0,\ldots,x_n]$ is natural because we don't really know how to define other kind of functions, $X$ is defined by its ideal $I$ and we can recover $I$ from $X$, and for $k = \mathbb{C}$, $X$ a smooth projective curve it is a theorem that all the meromorphic functions are rational. – reuns Dec 26 '17 at 07:39
  • @AaronJohnson Using the given link: $f$ can be extended to a morphism $f': X \longrightarrow Y$, and $g$ can be extended to a morphism $g': Y \longrightarrow X$. Then $f'\circ g'$ and $g'\circ f'$ are both identity on dense open sets, and hence identity on the whole space. – Krish Dec 26 '17 at 15:22
  • I think I understand now, thanks! – Aaron Johnson Dec 26 '17 at 22:00

1 Answers1

0

Here is another way without the use of coordinates, 'adapted' and expanded from the proof of Hartshorne's Theorem II.8.19.

Let $U\subset X$ be the largest open subset for which there is a morphism $f:U\to Y$ representing the birational map. Let $P\notin U$ be a point. Since $X$ is irreducible of dimension 1, the only non-closed point is the generic point, which must be contained in $U$. In other words, $P$ has to be closed, of codimension 1. By the regularity of $X$, $\mathcal O_{P,X}$ is a regular local ring of dimension 1, so it is a valuation ring. Let $K$ be its field of fractions. We have the commutative diagram, where $\operatorname{Spec} K\to U$ is the generic point. Since $Y$ is projective, in particular, proper, there exists a unique dashed morphism as such.

1

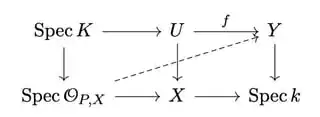
Since the diagram commutes, the dashed map $g$ is compatible with the original birational map $f$. (They coincides at the generic point.) Take an open affine neighborhood $V=\operatorname{Spec}A$ of $g(P)\in Y$, also an open affine neighborhood $U=\operatorname{Spec}B$ of $P\in X$. Then $g$ is locally a $k$-algebra homomorphism $\varphi:A\to \mathcal O_{P,X}$, where $\mathcal O_{P,X}=B_P$. Since $Y$ is of finite type over $k$, $A$ is a finitely generated $k$-algebra. Suppose the generators are $a_1,\ldots,a_n\in A$, we may write $\varphi(a_i)=b_i/s_i$ for $b_i,s_i\in B$ and $s_i\notin P$. Let $s=s_1\cdots s_n$. Then $\varphi$ restricts to a map $A\to B_s$, which corresponds to a morphism of schemes $D(s)\to V$. Again since this map is the same as the given $f$ at the generic point, there exists some open $Z$ such that $g\vert_Z=f\vert_Z$, which contradicts the maximality of $U$. Thus $U=X$.

Similarly, we may prove that $Y\to X$ is a regular map, and hence $X$ and $Y$ are isomorphic.

Peter Griffin
  • 184