The area of a right spherical triangle

Question

Is there a compact formula for the area (excess angle – assuming a unit sphere) of a right spherical triangle given its side lengths $a$ and $b$?

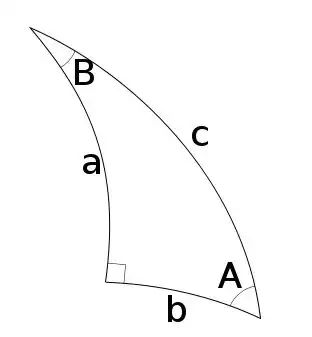
As explained in an answer to an earlier question about the area of a generic spherical triangle, the excess angle $E$ is given by $$\tan\frac E4=\sqrt{\tan\frac{a+b+c}4\tan\frac{-a+b+c}4\tan\frac{a-b+c}4\tan\frac{a+b-c}4}$$ However, I do not have $c$. Of course, I can use Napier's rules for right spherical triangles to find $c$.

I thought about using integration in spherical coordinates (assuming B is the north pole and equating $a$ and $c$ with polar and azimuthal angles respectively). That approach, however, requires knowing the exact representation of the great circle that connects $A$ to $B$ in the coordinate chart.

Note that there is also the equivalent of the Pythagorean Theorem (Theorem 4.3) to get $c$: $$\cos(c)=\cos(a)\cos(b)$$ — robjohn, Dec 10 '17 at 12:56

score 9 · Accepted Answer · answered Dec 10 '17 at 04:48

9

In Theorem 9.2 of this document, it is shown that the area of a spherical right triangle, $E$, is given by $$ \tan\left(\frac E2\right)=\tan\left(\frac a2\right)\tan\left(\frac b2\right) $$ where $a$ and $b$ are the two legs of the right spherical triangle.

answered Dec 10 '17 at 04:48

robjohn

353,833

Wow. I didn’t know that. Much swifter than my primitive method. – Lubin Dec 10 '17 at 04:49

score 7 · Answer 2 · answered Dec 10 '17 at 04:46

7

Napier’s Rules do it easily. The Rule that helps you is $\sin b=\tan a\cot A$, in other words, \begin{align} \tan A&=\frac{\tan a}{\sin b}&A&=\arctan\left(\frac{\tan a}{\sin b}\right)\,,\\ \tan B&=\frac{\tan b}{\sin a}&B&=\arctan\left(\frac{\tan b}{\sin a}\right)\,,\\ \text{area}&=A+B-\frac\pi2\,. \end{align}

answered Dec 10 '17 at 04:46

Lubin

65,209

1

(+1) I think this can be worked into the formula in my answer. – robjohn Dec 10 '17 at 04:57
Very likely, @robjohn. I was just too lazy to try. – Lubin Dec 10 '17 at 05:21

score 6 · Answer 3 · edited Dec 10 '17 at 08:09

6

According to Todhunter's Spherical Trigonometry (section VIII example 4): $$\sin\frac E2=\sin\frac a2\sin\frac b2\sec\frac c2$$ $$\cos\frac E2=\cos\frac a2\cos\frac b2\sec\frac c2$$ Then $$\tan\frac E2=\tan\frac a2\tan\frac b2$$ According to item 99 of the same source, $E=A+B+C-\pi$ for any triangle on the unit sphere. When $C=\frac\pi2$: $$E=A+B-\frac\pi2$$

edited Dec 10 '17 at 08:09

Jeppe Stig Nielsen

5,419
23
31

answered Dec 10 '17 at 04:49

Parcly Taxel

105,904

(+1) If you look at example 4. in section VIII (p.78) and divide the formula for $\sin\left(\frac12E\right)$ by the formula for $\cos\left(\frac12E\right)$, you get the formula in my answer. – robjohn Dec 10 '17 at 04:56
@robjohn Worked in. – Parcly Taxel Dec 10 '17 at 05:02

The area of a right spherical triangle

3 Answers3