How to identify bipartite graph from Adjacency matrix?

Question

I have attached a picture of a bipartite graph with two different ways of naming vertices. The Adjacency matrix for the two is also attached. As can be seen...Except for zero in diagonals (since no loops)... the Adjacency matrix for the two looks different.

My question is ...Is there some property of adjacency matrix from which one can figure out if a graph is bipartite IRRESPECTIVE of how vertices are numbered?

Answer 1

You can use a quick algorithm to check whether it's bilateral.

You're given an adjacency matrix of order $2n$ (i.e. a representation of a graph with $2n$ vertices.)

1. Find the column with the most ones in it; suppose it's column $k$. Let $N_k$ be the list of ones in column $k$ (these are the neighbors of vertex $k$). Initialize a partition $P \equiv N_k$, and a partition $Q=\{k\}$.

2. [Loop.] Iterate over each column $j$ in the matrix:

   If $P$ has more than $n$ ones in it, the graph can't be bipartite. In that case, quit and return NOT BIPARTITE.

   Compute $N_j$. Now either:

   • $P$ and $N_j$ have no ones in common: $P$ is zero whenever $N_j$ is one, and vice versa. In this case, keep going to the next column.
   • $P$ and $N_j$ have some ones in common. Update $P = P \cup N_j$, and $Q = Q \cup \{j\}$, and go to the next column.

3. Once again, if $P$ has more than $n$ members, the graph can't be bipartite—quit and return NOT BIPARTITE.

4. If the graph really is bipartite, $P$ now contains a complete partition of the graph. Permute the adjacency matrix to put all the members of $P$ first, and all of the members of $Q$ last.

5. If the matrix is now in the canonical form of a bipartite adjacency matrix (where the upper-left and lower-right blocks are all zero), the graph is bipartite; quit and return BIPARTITE. Otherwise, the graph isn't bipartite — quit and return NOT BIPARTITE.

---

Here's how to use this algorithm. Take your second graph as an example, which has $2n$ vertices with $n=3$.

• Column 1 has three ones in it. Since this is the maximal number of ones in any column, we can use it as a starting point. Then $N_1 = \{2,4,6\}$, so we initialize $P=\{2,4,6\}$ and $Q=\{1\}$.
• We begin looping over the columns of the matrix.
• Column 1 overlaps with $P$, so $P \leftarrow P\cup N_1 = \{2,4,6\}$, and also $Q \leftarrow Q \cup \{1\} = \{1\}$.
• Column 2 doesn't overlap at all.
• Column 3 overlaps; $Q \leftarrow Q \cup \{3\} = \{1,3\}$.
• Column 4 doesn't.
• Column 5 does. $Q \leftarrow Q \cup \{5\} = \{1,3,5\}$.
• Column 6 doesn't.
• If this graph is bipartite (and it is), $P$ should now contain a partition of the graph. In fact, we know $P=\{2,4,6\}$ and $Q=\{1,3,5\}.$ If we permute the adjacency list to put members of $P$ first and members of $Q$ last, we find that it appears in canonical form.

Answer 2

There are a couple of algebraic tests that can be done with an $n\times n$ adjacency matrix $A$:

• For a bipartite graph, the diagonal of $A^{2n+1}$ will always be $0$, because there are no odd cycles. If the graph is not bipartite, then there will be an odd closed walk of length at most $2n+1$, so the diagonal of $A^{2n+1}$ will contain a nonzero entry.
• If $D$ is the diagonal matrix of vertex degrees, then the Laplace spectrum (the multiset of eigenvalues of $D-A$) is equal to the signless Laplace spectrum (the multiset of eigenvalues of $D+A$) if and only if the graph is bipartite.

Regarding the second of these: in general, while the number of $0$ eigenvalues of $D-A$ gives the number of components of the graph, the number of $0$ eigenvalues of $D+A$ gives the number of bipartite components; this proves the "only if" part. For the "if" part, when the graph is bipartite, then $D-A$ and $D+A$ are similar, and the change-of-basis matrix is a diagonal matrix with diagonal entries $+1$ for one side of the bipartition and $-1$ for the other. For more details, see this pdf.

Answer 3

I will borrow notation from the Wikipedia section linked in the comments.

If $A$ is the adjacency matrix of a bipartite graph whose two parts have $r$ and $s$ vertices, then there exists a permutation matrix $P$ such that $$A = P \begin{bmatrix}0_{r,r} & B\\ B^\top & 0_{s,s} \end{bmatrix}P^\top,$$ where $B$ is an $r \times s$ matrix.

This is just a fancy way of saying that you can "re-number" the vertices (i.e., permute the columns and rows of $A$) so that all vertices of each bipartition are together, and then the adjacency matrix becomes the block matrix above.

Answer 4

Compute $A^n$

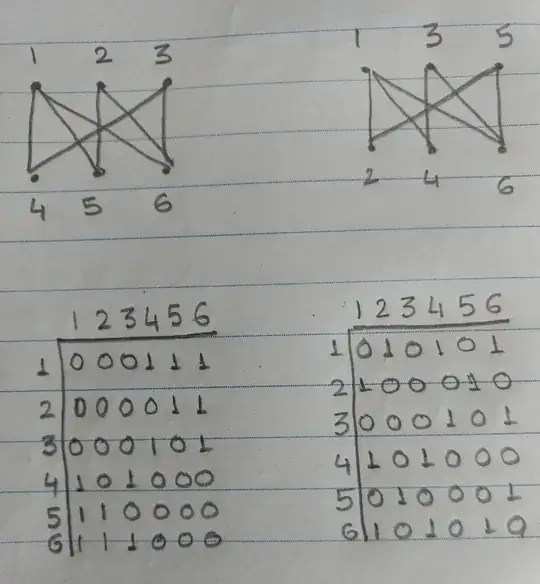
Given an $n\times n$ adjacency matrix $A$, compute $A^n$. If $A$ is bipartite then the rows of $A^n$ will have zeroes telling you what the partitions are. For example, for your matrix above,

$$A^{n} = \begin{bmatrix}0&1&0&1&0&1\\1&0&0&0&1&0\\0&0&0&1&0&1\\1&0&1&0&0&0\\0&1&0&0&0&1\\1&0&1&0&1&0\end{bmatrix}^6 = \begin{bmatrix}99&0&70&0&70&0\\0&50&0&49&0&70\\70&0&50&0&49&0\\0&49&0&50&0&70\\70&0&49&0&50&0\\0&70&0&70&0&99\end{bmatrix}$$

Notice the zeroes in each row of this matrix. There are exactly two patterns: zeroes in column (2,4,6) or zeroes in column (1,3,5). Every row matches one of the patterns, and the two patterns are complementary, meaning if you put them together you get all the nodes (1,2,3,4,5,6). This suggests that the nodes belong to two complementary partitions, (1,3,5) and (2,4,6). You can check the partitions to confirm the graph is bipartite.

Compute $A^{2n+1}$

By the same principle, you can compute $A^{2n+1}$. The zero entries of $A^{2n+1}$ will similarly suggest a bipartite partition, which you can check. Furthermore, the matrix $A^{2n+1}$ has the nice property that $A$ describes a bipartite graph if and only if every diagonal entry of $A^{2n+1}$ is zero.