3

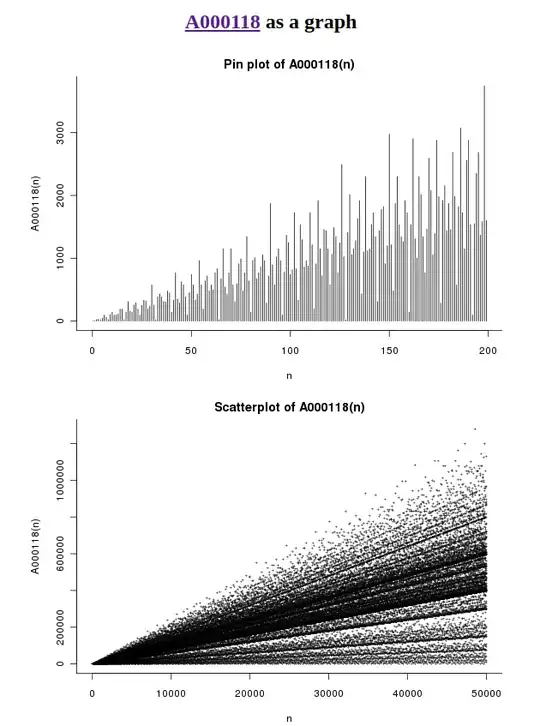
I found this result mentioned in passing in a number theory paper. It looks almost self-evident:

$$ \# \{ (a,b,c,d) \in \mathbb{Z}^4 : a^2 + b^2 + c^2 + d^2 = m\} \asymp m $$

It is stated without proof. It looks almost like the 4-squares theorem in fact that number is $r_4(m)$ which is A000118

enter image description here

This plot looks possibly linear, but with a bunch of noise. It doesn't look obvious.

cactus314
  • 25,084
  • https://math.stackexchange.com/questions/366673/express-integer-as-sum-of-four-squares – cactus314 Dec 05 '17 at 18:40
  • Where exactly in the paper is this mentioned? Do you mean the number of $4\times 4$-matrices on page $17$? – Dietrich Burde Dec 05 '17 at 19:16
  • @DietrichBurde Top of page 17 in this paper of Blomer and Pohl. Those matrices are in bijection with solutions to the 4-squares equation right? These well-known results, they mention in passing, are always news to me. – cactus314 Dec 05 '17 at 19:19

1 Answers1

1

By Jacobi's four-square theorem we have $$ r_4(n)​=\begin{cases}​8\sum\limits_{m|n}​m&​\text{if }​n\text{ is odd}​\\[12pt]​ 24\sum\limits_{\begin{smallmatrix}​ m|n \\ m\text{ odd}​ \end{smallmatrix}​}​m&​\text{if }​n\text{ is even}​. \end{cases}​​ $$ For $n=p$ prime this gives, for example, $r_4(p)=8(p+1)\asymp p$. In general, the asymptotic growth rate of $\sigma(n)=\sum_{m\mid n}m$ can be expressed by: $$ \limsup_{n\rightarrow\infty}\frac{\sigma(n)}{n\,\log \log n}=e^\gamma. $$ The behaviour of the sigma function is very irregular, as your plots also show.

Dietrich Burde
  • 140,055