9

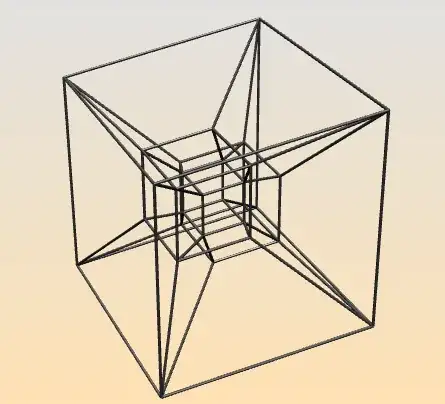
I was wondering what people call a certain type of shape. It is the shape formed by an orthogonal projection of a hypercube along one of its longest diagonals.

In other words, fill in the missing entries:

n-simplex : Triangle ->      Tetrahedon        ->  5-cell    ...    
 n-cube   :  Square  ->         Cube           -> Tesseract  ...  
   ?      :  Hexagon -> Rhomibic Dodecahedron  ->     ?      ...

IMPORTANT: I'm looking for the name of the class of shapes, not just the 4D analogue.

M. Winter
  • 30,828
Lucas
  • 1,519
  • It seems to me your arrows should point in the opposite direction---from right to left. – Michael Hardy Dec 10 '12 at 03:53
  • 2
    @MichaelHardy The arrows represent the well known coolness ordering of polytopes, read "X -> Y" as "Y is cooler than X". I think I get your intuition, there are increasing freedoms the way I drew them. e.g. the tetrahedron uniquely specifies the triangle, but not vice-versa. – Lucas Dec 10 '12 at 04:16

4 Answers4

7

What you are looking for is the vertex-frist projection of a hypercube. Apparently it seems that the 4d analogue has no special name.

You can read this post for more informations.

Edit: I computed the polytope. Read my blog post about it. Here is a teaser: enter image description here

A.Schulz
  • 3,828
3

I got here via A. Schulz's blog entry. As he says, you are looking for the projection of the $(d+1)$-dimensional hypercube (the $(d+1)$-cube for short) along a diagonal. But, actually, any generic projection of the $(d+1)$-cube will give (combinatorially) the same polytope. By "generic" I just mean that the direction of projection is not parallel to any coordinate hyperplane.

A different description is that your polytope is the zonotope obtained as the Minkowski sum of any set of $d+1$ generic vectors in $\mathbb R^d$, where generic means that no $d$ of them lie in a hyperplane.

Stefan Hansen
  • 26,160
  • 7
  • 62
  • 95
Paco Santos
  • 31
  • Can you please add a link to A. Schultz's blog entry? – MJD Mar 04 '13 at 14:14
  • The blog at least seems to be Aaron Schultz's, but I could not find the specific post. – MJD Mar 04 '13 at 14:17
  • It is not Aaron, but André Schultz. I did not add the link since he put the link in his answer, above (http://math.stackexchange.com/a/261323/64942). Anyway, the link is: http://ongraphs.de/blog/2013/02/vertex-first-projection-of-hypercubes/ – Paco Santos Mar 04 '13 at 20:41
1

Is there any chance that you are looking for the name of a {3,4,3} regular convex polychoron? It is called 24-cell (or icositetrachoron, octaplex, octacube polyoctahedron).

Solid orthographic projectionsWireframe Schlegel diagrams (Perspective projection)

24-cell can be derived as a rectified 16-cell (different from 16-cell).

all kinds of 16-cells

Other related polychrons (uniform, but not necessary regular and convex):

polychrons you may find useful

Or if you are looking for a {5,3,3} regular and convex 4D polytope, it is called 120-cell (or hecatonicosachoron).

Solid orthographic projections Wireframe Schlegel diagrams (Perspective projection)

Here is a table I found on Wikipedia that describes the polytope families. Hope you find it useful.

enter image description here

0

The polytopes you describe are the duals of a family of uniform polytopes. So, they are higher-dimensional analogues of the Catalan solids.

I have currently no better idea for how to describe these uniform polytope to you other than by their Coxeter diagrams:

$\qquad\qquad$

They belong to the $A_d$-family of uniform polytopes, that is, they have (an extended version of) the symmetry group of the $d$-simplex.

According to a link posted by A. Schulz, these polytopes are also called "cats-eye polytopes", which I think is pretty cool.

M. Winter
  • 30,828