Can a NFA reach two final states at the same time?

Question

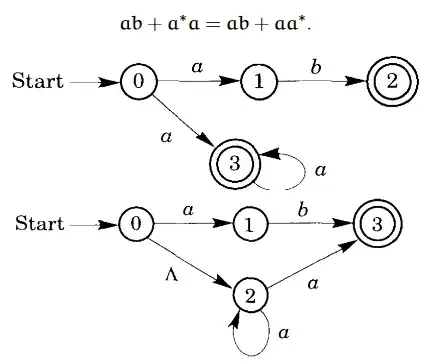
I'm studying nondeterministic finite automata, and I understand them in principle. Compared to deterministic FA, you can have more than one transition function with the same character starting from a single state and you can have "empty" transitions, and you can "choose" which one to follow based on the current string. So I came to an example which is confusing me.

So these two NFAs can recognize strings from the same alphabet. For example abaaaa.

What is confusing me is the first branch in both cases. For example in the first one something like this would happen:

Start, read a, go to 1, read b, go to 2, which is a final state, but the string isn't over. So what happens now? Does it go back to 0 and starts reading the final as? so 0, read a, go to 3, read a, go 3, read a, go 3, read a, go 3, finish?

Essentially, with NFA, can we follow two or more paths at the same time? (As if we "split" the string in two parts maybe?) Because otherwise I can't see how any string would be accepted in this case. ab would lead to state two, but the string isn't over, or a would lead to state 3, but then we would find b and the string would be rejected in that state.

In the second one how is the final state reached? We would still need to "go back" to 0.

Answer 1

The language accepted by an NFA is the set of all strings $s$ for which there exists an accept path in the NFA (meaning a path from the start state to an accept state) which is labelled by the letters of $s$ in order. You can't start over. You can't break the string into pieces and follow separate paths with separate pieces of the string. You have to start at the start state and look for paths along which you can read off each letter of the string one-at-a-time, and perhaps one of them will end with an accept state; if such a path exists, the string is accepted; if no such path exists, the string is not accepted.

So, for example, in your first automaton, let's consider a few examples.

First example: the string $aa$ is accepted, because there exists an accept path in that automaton labelled by $aa$, namely the path $0 \mapsto 3 \mapsto 3$. The fact that the path that starts $0 \mapsto 1$ cannot be continued is irrelevant.

Second example: the string $ab$ is accepted, because there exists an accept path in the automaton labelled by $ab$, namely the path $0 \mapsto 1 \mapsto 2$.

Third example: the string $abb$ is not accepted, because there does not exist any accept path in the automaton labelled by $abb$. You could start with $0 \mapsto 1 \mapsto 2$ labelled by the first two letters $ab$ of $abb$, but since you cannot continue with the third letter $b$, you're not going to get an accept path this way. Or you could start with $0 \mapsto 3$ labelled by the first letter $a$ of $abb$, but since you cannot continue with the second letter $b$, you're not going to get an accept path this way either. Since you have exhausted all of the possibilities for accept paths in the automaton labelled $abb$, and since you have demonstrated that none exists, it follows that $abb$ is not accepted.

Fourth example: consider the string $a$. You could start with the path $0 \mapsto 1$, and you're done with the string, but oops, you're not at an accept path; so there's no accept path for the string $a$ which starts with $0 \mapsto 1$. No worries, though, because instead you start with the path $0 \mapsto 3$, and the string is done and you're at an accept state, and so the string $a$ is accepted.