The old series for $\pi$ is this alternating series:
$$\pi = 4 \sum_{i=0}^{\infty}\frac{(-1)^i}{2i+1}$$
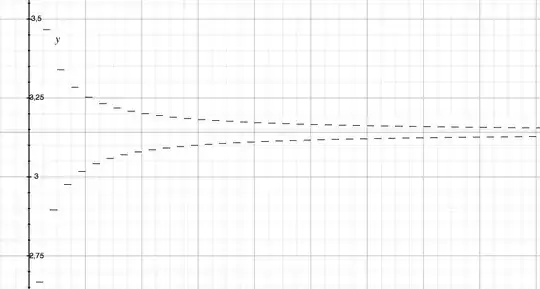
Now, as already noticed, the series is alternating: adding one term overshoots $\pi$ every time. The partial sums evolve like this:
Now, I thought: let's average the partial sum K and partial sum K+1. This will converge faster, right? The result is this:
Where the original series is still visible in light grey. Indeed this is a success! It converges faster. But wait! It again is an alternating series. So we can repeat this trick over again. I did all the maths and it turns out you can keep repeating this trick for ever. Which basically causes you to be able to construct a series expansion for $\pi$ with arbitrary convergence speed.
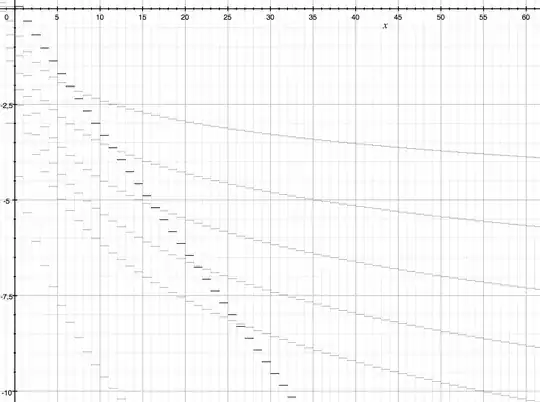
I plotted the $log(abs(\pi-s_n(k)))$ functions for some of these series:
In the figure above, the selected graph is the Euler Transformed variant:
$$\pi = \sum_{n=0}^{K}{\frac{\left( n! \right)^{2}2^{n+1}}{\left( 2n+1 \right)!}}$$
The fastest converging one on this figure is the one obtained after applying this trick 10 times (I wrote some Haskell to calculate this):
$$s_{10}\left( k \right)= 4\sum_{i=0}^{k}{\frac{\left( -1 \right)^{i}}{2i+1}} +\; \left( -1 \right)^{k}\; \left( \; -\; \frac{\left( 3.99609375 \right)}{\left( 2k+3 \right)}\; +\; \frac{\left( 3.95703125 \right)}{\left( 2k+5 \right)}\; -\; \frac{\left( 3.78125 \right)}{\left( 2k+7 \right)}\; +\; \frac{\left( 3.3125 \right)}{\left( 2k+9 \right)}\; -\; \frac{\left( 2.4921875 \right)}{\left( 2k+11 \right)}\; +\; \frac{\left( 1.5078125 \right)}{\left( 2k+13 \right)}\; -\; \frac{\left( 0.6875 \right)}{\left( 2k+15 \right)}\; +\; \frac{\left( 0.21875 \right)}{\left( 2k+17 \right)}\; -\; \frac{\left( 4.296875\times10^{-2} \right)}{\left( 2k+19 \right)}\; +\; \frac{\left( 3.90625\times10^{-3} \right)}{\left( 2k+21 \right)} \right)$$
The nice thing about this is that it requires only 10 additional terms, for significant faster convergence and that the rest remains the same.
Now this was a lot of fun, but:
- Does this technique have a name?
- Is this result of any significance, as I seem to be able to reach arbitrary rate of convergence, at virtually the same cost?
- Other series are still faster, I think, because the $log(abs(∆))$ plots get flat after a while, in comparison to the Euler Transformation variant.