1

I got this challenge question on brilliant.org: $\int_{0}^{\pi/4}\sqrt{\tan x} dx$

I first used, $\int_{0}^{\pi/4}\sqrt{\tan(\pi/4-x)} dx$ which simplifies: $\int_{0}^{\pi/4}\sqrt{\frac{1-\tan x}{1+\tan x}} dx$

Then, I used Weierstrass's substitution by using $t=\tan(\frac{x}{2})$ and $dx=\frac{2}{1+t^2}$ and simplified: $2\int_{0}^{\tan(\pi/8)}\frac{1-t}{(1+t)(1+t^2)} dx$

After some manipulation, I calculated the integral to be $I=2\ln(\tan(\frac{x}{2}))-\ln(1+t^2)+c$ and $I(\pi/4)-I(0)=0.53$

But Desmos tells something different: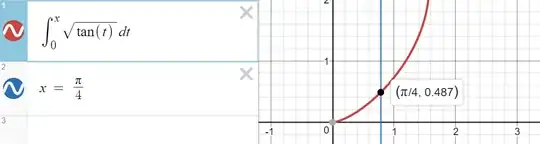enter image description here

Have I done something wrong? I have rechecked a few times. But I find no error!

Jack D'Aurizio
  • 361,689
Partha Sarker
  • 547

2 Answers2

2

With $x\mapsto \pi/4-x$ you get $$ \int_0^{\pi/4}\sqrt{\tan x}\,dx = \int_0^{\pi/4}\sqrt{\tan(\pi/4-x)}\,dx = \int_0^{\pi/4}\sqrt{\frac{1-\tan x}{1+\tan x}}\,dx $$ If $t=\tan(x/2)$, we have $\tan x=2t/(1-t^2)$, so $$ \frac{1-\tan x}{1+\tan x}= \frac{1-\dfrac{2t}{1-t^2}}{1+\dfrac{2t}{1-t^2}}= \frac{1-2t-t^2}{1+2t-t^2} $$ which bears no similarity with your computation.

egreg
  • 244,946
0

with $$t=\sqrt{\tan(x)}$$ we get $$2tdt=(1+\tan(x)^2)dx=(1+t^4)dx$$ thus $$dx=\frac{2dt}{1+t^4}dt$$ not that $$\tan(x)'=\frac{1}{\cos(x)^2}=\frac{\sin(x)^2+\cos(x)^2}{\cos(x)^2}$$

Dr. Sonnhard Graubner
  • 97,058