Why do we care about equivalence relations?

Question

I understand that equivalence relations can group elements of a set to a class that share similar properties. I think it's really cool that we can partition a set using equivalence relations. I'm also someone who doesn't do math for its applications but for its beauty. However...

Why do we care about equivalence relations?

For a specific equivalence relation reflexivity, symmetry, transitivity are always immediate (at least from what I have seen). You can e.g. define modulo with equivalence relations. Suppose you have never even heard of the equivalence relations, though. You could still define modulo without a problem.

Example: Just today, we've defined connected components of a graph using equivalence relations in class. Why would you want to do that? Why not use standard graph theory language? I don't see the reason for using equivalence relations to introduce connected components - what exactly is it that we gain by introducing equivalence classes?

So in summary, I kind of lack a motivation for equivalence relations and would appreciate examples that could enlighten me on that.

Answer 1

In the context of the connected components of a graph, the idea isn't very interesting, because the picture for connected components of a graph is already so clear and easy to understand geometrically.

But one of the principal techniques of mathematics is to find the underlying structure in one context, and then try to make an abstract model of it that might apply in other contexts as well. By doing this, we understand the connections between the two contexts, and we can sometimes solve difficult problems in one context by applying tools imported from some other context.

We don't formulate the idea of a partition or an equivalence relation because we want to study the connected components of graphs. For that it's unnecessary, because graph components are simple.

But that simplicity makes graph theory a good place to start understanding the idea of an equivalence relation, so that when you happen across it in a different context, where it might be more useful, you can recognize it and say “oh, we can model this with an equivalence relation, which means that it partitions the structure into components, and I already know some theorems about how that will work and some techniques I can use.”

And you have a language for talking about these things, which can be applied in many different situations, so that when you say “consider the equivalence classes of (something) under (some relation)” you and the people you are talking to instantly get an idea of what is going on: these classes are disjoint, every object is in exactly one class, and so on, just like the components of a graph.

Examples

1. What are fractions? They are notations of the form $\frac ab$, where $a$ and $b$ are integers, and $b$ is not zero. What are the rational numbers? Just fractions? No, they are the equivalence classes of fractions under the relation that says $\frac ab \equiv \frac cd$ if $ad=bc$, because for example $\frac 36$ and $\frac8{16}$ are the same rational number. Okay, big deal, we already know all about rational numbers. But having identified the process, we can now apply it to all sorts of things more complicated than the integers. Can we do the same construction for, say, polynomials? (We can!) Are the results useful and interesting? (They are!)

2. We can relate the complex numbers to polynomials by defining each complex number as a part of a partition induced on the set of polynomials by a certain equivalence relation. By using different equivalence relations we can define different systems analogous to the complex numbers and use them to study properties of polynomials.

3. Mathematics has a structure called a group, which is a model of a way in which a thing can have symmetry. There is an important “quotient” operation on a group which arises when you consider certain symmetries to be “equivalent”; the quotient is a group that describes the symmetries of the resulting equivalence classes.

4. This is a very specific example: Consider some geometric object which has an even number of symmetries. Then the object must have at least one symmetry which is an “involution”: this means that if you perform the symmetry exactly twice, the object is back in its original position. Objects without involutions must have an odd number of symmetries! (An example is a table-saw blade with 37 teeth.) I hope this is not obvious! But it is very easy to show if you consider the right equivalence relation on the symmetries.

5. An important technique in physics is to analyze the symmetries of the universe itself. For example, the laws of conservation of momentum and energy are consequences of certain symmetries of space-time. The abstract structure of spaces with these symmetries is often best understood as a particular quotient group.

6. This “quotient” idea applies in other situations too. Many kinds of mathematical structures are best understood as quotients, in this sense. For example, in topology we often view a circle as being a quotient of a line segment, under the equivalence relation that says that the two endpoints are equivalent. When we want to deal with a Möbius strip, we often formulate it as a certain quotient of a rectangle, where the equivalence relation makes certain points on the edge of the rectangle equivalent. Many related objects, much weirder than the Möbius strip, can be dealt with similarly.

We don't study the identification between partitions and equivalence relations just because it is cool. It is also useful in understanding other things. Partitions and equivalence relations pop up everywhere. Sometimes the partition is obvious, but the equivalence relation is easier to understand; then it is helpful to reinterpret the partition as an equivalence relation. Sometimes it is useful to go in the other direction instead.

Answer 2

One thing I haven't seen mentioned yet: Equivalence relations give us a tool for removing distinctions we are not interested in, so that the ones we are studying are all that remain.

For example, in topology it is very common to construct a new topological space by gluing existing ones together. MJD touches on this, but didn't show the power. Look at a square sheet. I would like to glue the two sides together:

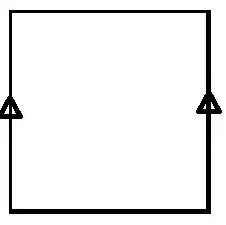
How do you do that in topology? By equivalence relation! If $S = [0,1]\times[0,1]$ is the square, then I define $$(x_0,y_0) \sim (x_1, y_1) \iff y_0 = y_1 \text { and } (x_0 = x_1 \text{ or } |x_0 - x_1| = 1)$$ Points in the middle or top and bottom of the square are equivalent to only themselves, but points on the LH side is equivalent to points on the RH side at the same height. I drop to the set of equivalence classes $S/\sim$, and note that it has been proven that topologies are compatible with any equivalence relation, and I'm done! Just by putting together that equivalence relation, I've defined a cylinder complete with topology. But that isn't the end. With just a little twist, I get something different: $$(x_0,y_0) \sim (x_1, y_1) \iff (x_0,y_0) = (x_1,y_1)\text{ or } (|x_0 - x_1| = 1 \text{ and } y_0 = 1 - y_1)$$ Now the space of equivalence classes is the Möbius strip, completely defined as a topological space by that little bit.

In the original square I had distinctions that were not desirable (LH side vs RH side). So I created an equivalence relation that ignored those distinctions. By passing to the equivalence classes, I have now gotten rid of the unwanted distinctions while keeping what is useful.

I can also glue the top and bottom sides together:

• if both top and bottom are glued straight and right and left are glued straight, you get the torus.
• if the top and bottom are glued straight, but the right and left are glued twisted, you get the Klein bottle.
• If both top and bottom and right and left are glued with twists, you get the projective plane.

And if you just make all boundary points equivalent to each other, then the entire boundary collapses to a single point, and you get the sphere.

This is just a tiny taste of the power of this technique. Every compact surface without boundary can be built by cutting a bunch of holes in a sphere, and then to each hole, either glue a torus with a single hole in it (gluing the borders of the two holes together), or else glue the border of a Möbius strip to the border of the hole.

Similar examples can be found in any field of mathematics. I was originally going to use building the tangent space in differential geometry, but switched to surfaces as being more accessible.

Equivalence relations are one of the most powerful tools in the mathematician's tool box. You will find them used everywhere.

Answer 3

One instance in math where the notion of an equivalence relation is particularly useful, and makes the axioms of an equivalence relation seem natural, is considering a set modulo some equivalence relation.

It is also useful when you have some sets with some type of structure (groups, rings, topological spaces) and you want some way to think of them as being the same. We usually do this by defining an appropriate 'structure preserving function' between them and intuitively these functions should satisfy the axioms of an equivalence relation. Otherwise, what use would it be to have 3, say topological spaces, A,B,C such that we regard A and B as the same B and C as the same but not A and C as the same.

In short an equivalence relation is a nice way to make precise the manner in which we can regard two things as the same (even if they are not "equal"). For the laymen example suppose I am talking about all the shoes I own, but I don't want to talk about distinct shoes, I just want to talk about all the pairs of shoes I own. My blue nike that goes on my left foot is not actually the same shoe as my blue nike that goes on my right foot, but if I consider my shoes modulo the equivalence relation that they belong to the same pair - both of my blue nikes just became the same shoe. In essence I can talk about, or prove things about, both shoes by just considering one of them. Because modulo the equivalence relation, they are "equal".

Edit: added after original post. Also, something I noticed as I was advancing into higher more abstract mathematics (which I am still doing!) was a common theme of certain math concepts. We love to take some normal concept such as 'equality' or 'distance' and say 'what are the properties that are inherent to distance' or 'what are the properties that are inherent to the notion of equality'. If you sit down and brainstorm for each, you will likely come up with the axioms for a metric space in the distance case, and the axioms of an equivalence relation in the equality case. Then, mathematicians love to say 'what happens in the more general setting where more general objects obey these properties?'. In this sense, the "motivation" would be more along the lines of curiosity. Then, if the theory is turning out to be fruitful and producing interesting results, that further motivates the study of this new 'generalized' notion. I actually haven't studied graph theory, so I can speak to much about your example regarding connected components, but my hunch is that using the equivalence relation is 'just general enough' in the sense that, by avoiding using an equivalence relation you could, at some point, be limiting your self by not being general enough or get wacky results because things are too general. Me personally, everything I study is algebraic - and equivalence relations are imperative. They help to study smaller algebraic structures without forgetting the old structure it came from - and again help make precise what it means for two algebraic structures to be equal.

Answer 4

Equivalence relations are a way to describe objects that are effectively the same in a given context.

If for some problem you find the solution $x \equiv 1 \pmod 6$, then you immediately know that the solution set is $\{6k+1 : k\in\Bbb Z\}$, and it's conceptually much cleaner and more intuitive to refer to the equivalence relation than to some theorem on modular arithmetic.

Keeping with the integers modulo $6$, imagine an infinite graph with vertices labelled with integers, and $uv \in E$ if $u \equiv v \pmod 6$. Then there will be six connected components, each corresponding to an equivalence class. If you zoom out far enough, then each of these components looks like a single object, and it is more interesting to look at how these objects relate to each other than to look at the infinitely many (but effectively the same) possible details.

Answer 5

An equivalence relation is a very basic kind of structure that occurs all through different areas of mathematics. You've mentioned two examples: modular arithmetic and connected components of graphs. There are many others. Yes, it would be possible to develop each one by itself without using the term "equivalence relation". But mathematicians are supremely lazy: they don't like to duplicate effort. And once you have the concept of equivalence relation, all you have to do is recognize that something is an equivalence relation and a whole set of tools is automatically available without further effort.

Answer 6

Although pretty much everything that needs to be said has already been addressed (much of it in MJD's excellent answer), I thought I'd share an excerpt from Princeton's Companion to Mathematics that was very helpful to me when I first encountered equivalence relations, equivalence classes, and all that jazz.

There are many situations in mathematics where one wishes to regard different objects as "essentially the same," and to help us make this idea precise there is a very important class of relations known as equivalence relations. Here are two examples. First, in elementary geometry one sometimes cares about shapes but not about sizes. Two shapes are said to be similar if one can be transformed into the other by a combination of reflections, rotations, translations, and enlargements. (See the similar shapes in the figure below.)

The relation "is similar to" is an equivalence relation. Second, when doing arithmetic modulo $m$, one does not wish to distinguish between two whole numbers that differ by a multiple of $m$: in this case one says that the numbers are congruent (mod $m$); the relation "is congruent (mod $m$) to" is another equivalence relation.

What exactly is it that these two relations have in common? The answer is that they both take a set (in the first case the set of all geometrical shapes, and in the second the set of all whole numbers) and split it into parts, called equivalence classes, where each part consists of objects that one wishes to regard as essentially the same. In the first example, a typical equivalence class is the set of all shapes that are similar to some given shape; in the second, it is the set of all integers that leave a given remainder when you divide by $m$ (for example, if $m=7$ then one of the equivalence classes is the set $\{\ldots,-16,-9,-2,5,12,19,\ldots\}$).

An alternative definition of what it means for a relation $\sim$, defined on a set $A$, to be an equivalence relation is that it has the following three properties. First, it is reflexive, which means that $x\sim x$ for ever $x$ in $A$. Second, it is symmetric, which means that if $x$ and $y$ are elements of $A$ and $x\sim y$, then it must also be the case that $y\sim x$. Third, it is transitive, meaning that if $x$, $y$, and $z$ are elements of $A$ such that $x\sim y$ and $y\sim z$, then it must be the case that $x\sim z$. (To get a feel for these properties, it may help if you satisfy yourself that the relations "is similar to" and "is congruent (mod $m$) to" both have all three properties, while the relation "$<$," defined on the positive integers, is transitive but neither reflexive nor symmetric.)

One of the main uses of equivalence relations is to make precise the notion of "quotient" constructions [as alluded to in MJD's answer].

Answer 7

There are a lot of great answers in here, but I thought I would include an important equivalence relation that arises in linear algebra.

If $A$ and $B$ are $n \times n$ matrices (over a field $F$), we say that $A$ and $B$ are similar and we write $A \sim B$ if there exists an invertible matrix $P$ such that $A = P^{-1}BP$.

When two matrices are similar, they represent the same linear transformation though possibly using different bases. If $A$ and $B$ are similar, then they represent the same underlying linear transformation and so $A$ and $B$ have the same rank, eigenvalues, determinant, trace, minimal polynomial, etc.

So why might we care about this? Well it can make computations easy for one. If you are presented with a matrix, you can determine what the underlying linear transformation is and there is often an "optimal" basis to represent that linear transformation that makes the corresponding matrix as simple as possible (i.e. lots of zeros). You can then use that particular matrix to do all of the computations you have in mind and save your self some time.

Answer 8

Equivalence relations are important because of the fundamental theorem of equivalence relations which shows every equivalence relation is a partition of the set and vice versa. Because partitioning is a very common idea in both pure and applied mathematics equivalence relations occur naturally but have the added benefit of allowing you to exploit the transitive, reflexive and symmetric properties of the relation.

I would also point out that "standard graph theory language" as you called it is to use equivalence relations. Very few theorems in mathematics are given the title "fundamental" and they show up in algebraic settings, logic, and even cutting and pasting surfaces together. It's very powerful and widely applicable modelling tool which is why they're ubiquitous in higher mathematics.

Answer 9

One common constructions of the real numbers involve equivalence relations:

The equivalence classes of Cauchy sequences of rationals under $\approx$, where for any sequences $f,g \in \mathbb{N} \to \mathbb{Q}$ we have $f \approx g$ iff $f(n)-g(n) \to 0$ as $n \to \infty$.

Furthermore, this is the only way to obtain a completion of a metric space in general.

But there are also many nice examples of equivalence relations in graph theory and topology:

1. Existence of a cycle containing given edges in an undirected graph. Each equivalence class forms the edges of a 2-connected component.

2. Existence of a cycle containing given vertices in a directed graph. The equivalence classes are called strongly connected components.

3. The isomorphism between given finite graphs. A major open problem is whether the Graph Isomorphism Problem (to decide whether the given pair of graphs are isomorphic) is in P or NP-complete or neither.

4. Whether given closed directed curves in the plane can be continuously deformed from one to the other without crossing the origin. The equivalence classes are exactly those determined by the winding number around the origin.

5. Whether given non-self-intersecting closed curves in 3-dimensional space can be continuously deformed from one to the other without self-intersection. It turns out that this is equivalent to the equivalence relation on the knot diagrams under Reidemeister moves.

Answer 10

We care about equivalence relations specially because one of the goals of mathematics in general is to classify objects, and, when you have an heuristically point of view, you can synthesize it in an abstract formulation, which will be useful to classify objects. For example, this notion of equivalence is useful to classify the "equivalence classes" modulo some fixed integer, but also is useful to determine the stalk of a sheave, and, as the underlying process is the same, you can relate equivalence classes of everything via functions or even functors. And, in some context, to prove the properties is not quite easy, for example, when you are trying to give a group structure to rational points over an elliptic curve, the associativity is a little bit difficult. That's the reason why we care about equivalence relations: classify.

Answer 11

Equivalence relations help generalize/relax the notion of equality, whereby you consider to be 'equal' (under the equivalence relation) elements that are in the same equivalence class. Equivalence relations are also used to construct quotient spaces (eg. in ring theory, in topology), which are ubiquitous in math (eg. the real numbers are a quotient space, the rational numbers are a quotient space; even the integers are a quotient space!).

Answer 12

There are even equivalence relations in Euclid, including congruence of triangles and similarity of triangles, as well as several theorems which give you conditions for checking congruence and similarity.

There's even a passage early in Euclid where he lists the properties of "equality", but when you see how these properties are used in Euclid then you see that these properties are actually being used (in modern language) as the definition of equivalence relations.

Answer 13

Equivalence relations generalize the concept of equality to different contexts. Suppose you are arranging your books. You decide to put the books with the same colour in the same bookshelf. In this scenario, you only care about what colour (assuming a book can be assigned a single colour without any ambiguity) a book is. So a blue science fiction novel and a blue book on abstract algebra are no different. They're both blue books.

Here, we have defined : Book X ~ Book Y iff they have the same colour.

Answer 14

As mentioned in this answer, we care about equivalence relations because an equivalence relation $\sim$ on a set $X$ naturally determines a corresponding partition $P$ of $X$. But this raises the obvious next question: Why do we care about partitions?

Often (but not always) when studying a particular set $X$, we need to consider the elements $x \in X$, but not the elements $y \in x \in X$. A partition $P$ of $X$ achieves the same thing. We do not need to concern ourselves with the underlying elements of a given $p \in P$. We can use these elements $x \in p \in P$ if we want to, but they don't get in the way.

This property is the reason partitions are so important. And the fact that $X$ is the disjoint union of the sets $p \in P$ (by definition of partition) is the reason this property applies. Formally, it is the universal property of the coproduct, which is the disjoint union in the category of sets. Informally, the disjoint union is the "most general" way to combine a collection of sets $p \in P$ to get a set $X$. No information about the elements of the sets $p \in P$ is relevant, only the sets $p$ themselves. Contrast this to the case of a standard (non-disjoint) union, in which the result depends on whether or not the sets involved have common elements.

So the partition is a tool for "zooming out" from the elements $x \in X$ in a way that allows us to no longer worry about those original elements at all, and instead focus only on a larger scale structure on $X$, namely $P$.