The whole set of equilateral triangles inscribed in a unit square $ABCD$ can be generated through the following procedure:

- Pick a point $P\in AB$;
- Rotate $ABCD$ by $60^\circ$ counter/clockwise around $P$;
- Consider the suitable intersections between $ABCD$ and the rotated squares.
By symmetry it is pretty clear that the minimum area of the inscribed equilateral triangle is attained when $P$ is the midpoint of $AB$ and the maximum area is attained when a vertex of the inscribed equilateral triangle is a vertex of the original square. In the former case the mentioned triangle has unit side length, in the latter the side length equals $\frac{1}{\cos 15^\circ}=\sqrt{6}-\sqrt{2}$.
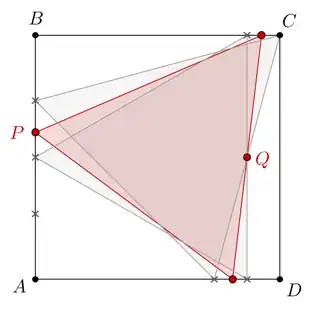
It is interesting to point out that if $P$ is a vertex of an inscribed equilateral triangle close to the midpoint of $AB$, the opposite sides goes through a fixed point $Q$, and the area of the inscribed equilateral triangle just equals $\frac{1}{\sqrt{3}} PQ^2$. Here it is an animation, too:



