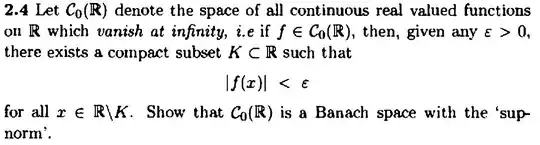Here is a question I was trying to solve:
My attempt:
Let $(f_n)$ be a Cauchy sequence in $(\mathcal C_0(\mathbb R),||.||_\infty).$ Then for each $x\in\mathbb R$ $(f_n(x))$ is a Cauchy sequence in $\mathbb R$ and hence convergent.
Define $f:\mathbb R\to\mathbb R$ by $f(x)=\lim_{n\to\infty}f_n(x).$ To show that $f\in\mathcal C_0(\mathbb R)$ and $||f_n-f||_\infty\to0.$
1 $f\in\mathcal C(\mathbb R):$ Choose $\epsilon>0.$ Then $\exists~k\in\mathbb N$ such that $||f_m-f_n||_\infty<\epsilon/2~\forall~m,n\ge k.$
That is, $\forall~x\in\mathbb R,~|f_m(x)-f_n(x)|<\epsilon/2~\forall~m,n\ge k.$
That is, $\forall~x\in\mathbb R,~\lim_{n\to\infty}|f_m(x)-f_n(x)|\le\epsilon/2~\forall~m\ge k.$
That is, $\forall~x\in\mathbb R,|f_m(x)-f(x)|\le\epsilon/2<\epsilon~\forall~m\ge k.$
So $(f_n)$ converges uniformly to $f$ on $\mathbb R\implies f\in\mathcal C(\mathbb R).$
[2] $f$ vanishes at infinity: Choose $\epsilon>0.$ Then $\exists~k\in\mathbb N,$ such that $\forall~x\in\mathbb R,~|f_n(x)-f(x)|<\epsilon/2~\forall~n\ge k.$
That is $\forall~x\in\mathbb R,~|f_k(x)-f(x)|<\epsilon/2.$
Also there exists a compact subset $C$ of $\mathbb R$ such that $|f_k(x)|<\epsilon/2~\forall~x\notin C.$
So $|f(x)|\le|f_k(x)-f(x)|+|f_k(x)|<\epsilon~\forall~x\notin C.$
Thus $f\in\mathcal C_0(\mathbb R).$
[3] Choose $\epsilon>0.$ Then there exists $k\in\mathbb N$ such that $\forall~x\in\mathbb R,|f_n(x)-f(x)|<\epsilon/2~\forall~n\ge k.$
That is $\sup_{x\in\mathbb R}|f_n(x)-f(x)|\le\epsilon/2<\epsilon~\forall~n\ge k.$
So $||f_n-f||_\infty\to0.$ Hence $f_n\to f$ in $\mathcal C_0(\mathbb R).$
Please tell me whether my attempt is correct.