Minimize $\min_{f\in E}\left(\int_0^1f(x) dx\right)$

Question

Inspired by this question, I pose this following problem.

Let $E$ be the set of all nonnegative continuous functions $f:[0,1]\to \mathbb{R}$ such that $$f(x)\,f(y)\ge |x-y|\qquad\forall\{x,y\}\subset [0,1]$$

Find $$\min_{f\in E}\left(\int_0^1f(x) \,dx\right)$$

Answer 1

Integrating both sides with respect to x and y we get

$$\left(\int_0^1f(x) dx\right)^2= \int_0^1\int_0^1f(x)f(y)dxdy \ge\int_0^1\int_0^1 |x-y|dxdy= \frac13.$$ that is $$\int_0^1f(x)dx \ge \frac{1}{\sqrt3.}$$

I am still searching whether the min is attain or not.

Answer 2

Let $A=A(f)=\int_0^1f(x)\,dx$. By the AGM inequality, $$A=\frac12\int_0^1 \big(f(x)+f(1-x)\big) dx \ge \int_0^1 \sqrt{f(x)f(1-x)}\,dx \ge \int_0^1 \sqrt{|1-2x|}dx = \frac23.$$

Similarly, $$A=2\int_0^{1/2} \frac{f(x)+f(x+1/2)}2\, dx $$ $$\ge 2\int_0^{1/2} \sqrt{f(x)f(x+1/2)} \, dx\ge 2\int_0^{1/2}\sqrt{1/2}\,dx=\frac1{\sqrt2}.$$

Added 14 Nov.
This might or might not have been obvious all along, but not explicitly so to me until just now. Note that if $g_1$ and $g_2$ satisfy the constraints, then so does $g(x) = \sqrt{g_1(x)g_2(x)}$, and moreover, by the AGM inequality, $$\int_0^1 \sqrt{g_1(x)g_2(x)}\,dx\le \int_0^1 \frac {g_1(x)+g_2(x)} 2\, dx.$$ Given any admissible $h$, the functions $h_1(x) = h(x)$, $h_2(x)=h(1-x)$, and $f(x)=\sqrt{h_1(x)h_2(x)} = \sqrt{h(x)h(1-x)}$ are admissible, and $\int_0^1 f\le \int_0^1 h$. Hence one cannot beat functions of the form $\sqrt{h(x)h(1-x)}$, that is, functions that depend only on $|2x-1|$.

Another consequence of the AGM inequality is that if the minimum is attained, it is attained uniquely: Suppose $A(f)=A(g)$ where $f\ne g$. Then $A(h)<A(f)$, where $h(x)=\sqrt{f(x)g(x)}$.

Added 17 Nov.
Not only can one not beat functions of form $f(x)=\phi(|2x-1|)$ , but one cannot beat such functions where continuous $\phi:[0,1]\to\mathbb R^+$ is also required to be nondecreasing. The $f(x)f(y)\ge|x-y|$ constraint translates to a $\phi(u)\phi(v)\ge(u+v)/2$ constraint for $u,v\in[0,1]$. If $\phi$ obeys these constraints, so does monotonic $\phi^*(u)=\min\{\phi(t): t\in[u,1]\}$, for which the corresponding $A(f^*)\le A(f)$.

(I'm hoping to use a compactness argument somehow to then prove the minimum $A(f)$ is attained. I think that such an argument succeeds in the restricted problem where one sticks in an additional constraint $f(0)=\gamma$, but don't yet see yet why the restricted optimal value of $A$ depends continuously on $\gamma$.)

Answer 3

NOTE: Still not a complete answer, just improving on the lower bound.
EDIT: Added an improvement on the upper bound (a better function which "works").

I decided to combine the two ideas in kimchi lover's bounds, by putting a bound on $$ \int_0^1 f(x)dx = \int_0^{1/4} \left[f(x) + f(1-x) + f(1/2+x) + f(1/2-x)\right]dx $$ Considering the four values $(u,v,s,t) = (f(x), f(1-x), f(1/2-x), f(1/2+x))$ as independent, but satisfying the constraints $$ \begin{align} &uv \geq 1-2x \\ &ut \geq 1/2 \\ &sv \geq 1/2 \\ &st \geq 2x, \end{align} $$ I found a lower bound for $u+s+v+t$. (There are two more inequalities, of course, but the minimizing set of values turns out to be symmetric, $s = t$ and $u = v$, so the $us$ and $tv$ inequalities are weaker than the $ut$ and $sv$ ones.) The approach is rather brute-force: pick $u$ and $s$ as independent, consider the different cases for which of the inequalities involving $t$ and $v$ are the stronger ones, then minimize an expression in terms of $u$ and $s$. The calculations are tedious, and since this is not a complete answer anyway, I'll omit them. I got the following: $$ u + s + t + v \geq \frac{3-4x}{\sqrt{1-2x}}, $$ minimum attained at $u = v = \sqrt{1-2x}$ and $s = t = {1\over2u}$ (these are not too surprising, of course). Thus $$ \int_0^1 f(x) dx \geq \int_0^{1\over4} \frac{(3-4x)dx}{\sqrt{1-2x}} = {5-2\sqrt2\over 3} \approx 0.72386 $$ If we try to piece together a function from the $(u,s,t,v)$'s for $x \in [0,1/4]$, it still doesn't satisfy some of the constraints, such as for example $f(x)f(1) \geq 1-x$.

A function which does meet the constraints everywhere is $$ f(x) = \frac{e^{|2x-1|}}{\sqrt{2e}}. $$ That it does work can be verified using the triangle inequality $$ f(x)f(y) = \frac{e^{|2x-1|+|2y-1|}}{2e} \geq \frac{e^{2|x-y|}}{2e} \geq |x-y| $$ where the last one holds because $e^{2t} - 2et$ has a global minimum $0$ at $t = 1/2$. Its integral is $$ \int_0^1 \frac{e^{|2x-1|}}{\sqrt{2e}}dx = 2\int_{1/2}^1 \frac{e^{2x-1}}{\sqrt{2e}}dx = \frac{e-1}{\sqrt{2e}} \approx 0.73694 $$

EIDT: Following @kimchilover's idea to generalize the exponential function to $\beta e^{\alpha|2x-1|}$, the constraints will be satisfied if and only if the minimum of $$ \beta^2 e^{\alpha|2x-1|}e^{\alpha|2y-1|} - |x-y| $$ over $[0,1]\times[0,1]$ is non-negative. The strongest constraints are obtained using $x \in [0,1/2], y \in [1/2,1]$ so that we need $$ \beta^2 e^{2\alpha(y-x)} - (y-x) = \beta^2 e^{2\alpha t} - t \geq 0 $$ for $t \in [0,1]$. We can find the minimum, then if the minimum is in $[0,1]$, require that it is non-negative, or if it is outside, require that the closest "cut-off" is non-negative. Long story short, the optimal ones I found to be the root of $e^\alpha(\alpha - 3/2) + 3/2 = 0$, $\alpha \approx 0.874217$ (by Wolfram), $\beta = 1/\sqrt{2e\alpha}$, and for the integral $\approx 0.733001$.

Answer 4

Numerical experiment

The following numerical experiment yields, as we will see later, the correct assumptions for getting a good candidate for the optimum. Convexity will help us show that this candidate is indeed the optimum.

We plot the active set of the optimum of a discretization:

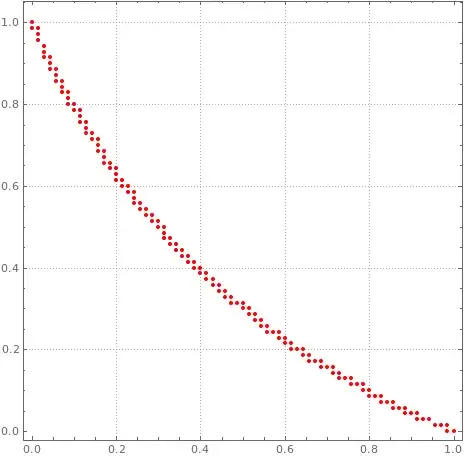
This is the output of the following code: activeset[k_] := Module[{h, constraints, vars, objective, optresult, result, pts}, h = 1/(2 k - 2); constraints = Flatten[Table[ Table[x[i] x[j] >= (2 k - i - j) h, {j, i, k}], {i, 1, k}]]; constraints = Join[constraints, Table[x[i] >= 0, {i, 1, k}]]; vars = Table[x[i], {i, 1, k}]; objective = Sum[x[i], {i, 1, k}] + Sum[x[i], {i, 2, k - 1}]; optresult = FindMinimum[{objective, constraints}, vars, Method -> "InteriorPoint"]; result = Table[{(i - 1) h, x[i]}, {i, 1, k}] /. optresult[[2]]; pts = Select[Flatten[Table[{i, j}, {i, 1, k}, {j, 1, k}], 1], Abs[x[#[[1]]] x[#[[2]]] - (2 k - #[[1]] - #[[2]]) h] < 10^(-5) /. optresult[[2]] &]; ListPlot[(pts - 1)/(k - 1), AspectRatio -> 1, PlotStyle -> Red, PlotTheme -> "Detailed"] ]; activeset[71]

Full solution

Set $S:=\{(x,y) \in [0,1]^2 : x+y \leq 1\}$. We define the maps \begin{alignat*}{2} &J : C[0,1] \rightarrow \mathbb{R},\quad &&J(u) := \int_0^1 \! \exp(u(x)) \, \mathrm{d}x, \\[1em] &I : C[0,1] \rightarrow C(S),\quad &&I(u)(x,y) := u(x)+u(y)-\log(2-x-y). \end{alignat*} We will study the optimization problems \begin{align} & \text{minimize} && J(u) \nonumber\\ & \text{subject to} && I(u) \geq 0, \tag{1} \\[1em] \text{and}\nonumber \\[1em] & \text{minimize} && \int_0^1 \! f(x) \, \mathrm{d}x \nonumber\\ & \text{subject to} && f \in C[0,1], \tag{2}\\ &&& f \geq 0, \nonumber\\ &&& f(x)f(y) \geq |x-y| \text{ for all } x,y \in [0,1]. \nonumber \end{align}

We will show that:

The unique solution $\bar{u}$ of $(1)$ is given by \begin{align*} \exp(\bar{u}(x)) &= \sqrt{2 \left(1+\sqrt{2}\right)}-\sqrt{2 x+\sqrt{2}-1}, \\[1em] J(\bar{u}) &= \frac{2}{3}\sqrt{1+\sqrt{2}}. \end{align*} The unique solution $\bar{f}$ of $(2)$ is given by \begin{align*} \bar{f}(x) &= \begin{cases} \dfrac{\exp(\bar{u}(2x))}{\sqrt{2}}&\text{if}\quad 0 \leq x \leq \frac{1}{2},\\ \dfrac{\exp(\bar{u}(2(1-x)))}{\sqrt{2}}&\text{if}\quad \frac{1}{2} < x \leq 1, \end{cases} \\[1em] \int_0^1 \! \bar{f}(x) \, \mathrm{d}x &= \frac{1}{3} \sqrt{2 \left(1+\sqrt{2}\right)}\quad (\approx 0.732456) \end{align*} where $\bar{u}$ is the unique solution of $(1)$.

Theorem 1 (Generalized Kuhn-Tucker Theorem).

Let $X$ be a normed space and $Y$ a normed space having positive cone $P$. Assume that $P$ contains an interior point.

Let $J$ be a Fréchet differentiable real-valued functional on $X$ and $I$ a Fréchet differentiable mapping from $X$ into $Y$. Suppose $\bar{u}$ minimizes $J$ subject to $I(\bar{u}) \geq 0$ and that $\bar{u}$ is a regular point of the inequality $I(\bar{u}) \geq 0$ i.e. there exists an $h \in X$ such that $I(\bar{u}) + I'(\bar{u})(h) > 0$. Then there is a positive functional $\psi \in Y^*$ such that \begin{align} J'(\bar{u}) &= \psi \circ I'(\bar{u}), \tag{3} \\\psi(I(\bar{u})) &= 0. \tag{4} \end{align}

Proof. See [Luenberger, David G, Optimization by vector space methods, Wiley, New York, 1969, p. 249]. $$\tag*{$\Box$}$$

Note: The following assumption (iii) is inspired by our numerical experiment.

Claim 1. If

(i) $\bar{u}$ is the solution of $(1)$

(ii) $\bar{u} \in C[0,1]$

(iii) there exists $g \in C^1[0,1]$ such that $$A:=\{(x,g(x)) : x \in [0,1]\} = \left\{(x,y) \in S : I(\bar{u})(x,y) = 0\right\},$$

then $g$ is an involution and $$\exp(\bar{u}(x)) = -g'(x)\exp(\bar{u}(g(x)))$$ for all $x \in [0,1]$.

Proof. By (iii) we have $I(\bar{u})(x,g(x)) = 0$ for all $x \in [0,1]$.

Since $I(\bar{u})(x,y) = I(\bar{u})(y,x)$ for all $x,y \in [0,1]$, we have $I(\bar{u})(g(x),x) = 0$ and thus $g(g(x)) = x$ by (iii) for all $x \in [0,1]$. Therefore $g$ is an involution.

We will now apply Theorem 1. The point $\bar{u}$ is regular, since $I'(\bar{u})(\mathbf{1}_{[0,1]}) = 2\cdot \mathbf{1}_S.$

Thus there exists a positive functional $\psi \in C(S)^*$ such that $(3)$ and $(4)$ are satisfied. Since $S$ is compact, there is a unique regular Borel measure $\nu$ on $\mathcal{B}(S)$ by the Riesz-Markov-Kakutani representation theorem such that $$\psi(v) = \int_S v(x,y) \, \mathrm{d}\nu(x,y)$$ for all $v \in C(S)$. We define a measure on $\mathcal{B}(S)$ by setting $$\mu(E) := \lambda\left(\{x \in [0,1] : (x,g(x)) \in E\}\right)$$ for all $E \in \mathcal{B}(S)$, where $\lambda$ is the Lebesgue measure on $[0,1]$. We will show that $\nu \ll \mu$, i.e. that $\nu$ is absolutely continuous with respect to $\mu$. Let $N \in \mathcal{B}(S)$ such that $\mu(N)=0$. By $(4)$ we have $\psi(I(\bar{u})) = 0$. Therefore $$\int_{S} I(\bar{u})(x,y) \, \mathrm{d}\nu(x,y) = 0,$$ and since $I(\bar{u}) \geq 0$, we have $\nu(S\setminus A)=0$ and $\nu(N \cap (S\setminus A))=0$. By $(3)$ we have $$\int_0^1 \exp(\bar{u}(x)) h(x) \, \mathrm{d}x = \int_S h(x) + h(y) \, \mathrm{d}\nu(x,y)$$ for all $h \in C[0,1]$. Set $N' = \{x \in [0,1] : (x,g(x)) \in N\}$. By definition of $\mu$ we have $\lambda(N') = 0$. Let $\epsilon > 0$. Then there exists $\bar{h} \in C[0,1]$ such that $\bar{h}(x) = 1$ for all $x \in N'$, $\bar{h}\geq 0$, and $\int_0^1 \exp(\bar{u}(x)) \bar{h}(x) \, \mathrm{d}x<\epsilon$. Now we have \begin{align*} \nu(N \cap A) &= \int_S \mathbf{1}_{N \cap A}(x,y) \, \mathrm{d}\nu(x,y) \\[1em] &= \int_S \mathbf{1}_{N'}(x) \, \mathrm{d}\nu(x,y) \\[1em] &\leq \int_S \bar{h}(x) + \bar{h}(y) \, \mathrm{d}\nu(x,y) \\[1em] &= \int_0^1 \exp(\bar{u}(x)) \bar{h}(x) \, \mathrm{d}x<\epsilon. \end{align*} Therefore $\nu(N \cap A) = 0$, thus $\nu(N) = 0$ and $\nu \ll \mu$. By the Radon–Nikodym theorem there exists a measurable function $w : S \rightarrow [0,\infty)$ such that $$\psi(v) = \int_S v(x,y)\, \mathrm{d}\nu(x,y) = \int_S v(x,y)\,w(x,y) \, \mathrm{d}\mu(x,y)$$ for all $v \in C(S)$. Since $\mu$ is the pushforward measure under $x \mapsto (x,g(x))$ we have $$\psi(v) = \int_0^1 v(x,g(x))\,w(x,g(x)) \, \mathrm{d}x$$ for all $v \in C(S)$. By $(4)$ we now have $$\int_0^1 \exp(\bar{u}(x)) h(x) \, \mathrm{d}x = \int_0^1 (h(x) + h(g(x)))\,w(x,g(x)) \, \mathrm{d}x$$ for all $h \in C[0,1]$. Since $g$ is a $C^1$-involution on $[0,1]$, we can substitute $g(x)$ for $x$ in $\int_0^1 h(g(x))\,w(x,g(x)) \, \mathrm{d}x$. We get $$\int_0^1 \exp(\bar{u}(x)) h(x) \, \mathrm{d}x = \int_0^1 h(x) (w(x,g(x))-w(g(x),x)g'(x)) \, \mathrm{d}x$$ for all $h \in C[0,1]$. Therefore $$\exp(\bar{u}(x)) = w(x,g(x))-w(g(x),x)g'(x)$$ for almost all $x \in [0,1]$. Since $g$ is an involution, we have \begin{align*} \exp(\bar{u}(g(x))) &= w(g(x),g(g(x)))-w(g(g(x)),g(x))g'(g(x)) \\[1em] &= w(g(x),x)-w(x,g(x)) \frac{1}{g'(x)} \\[1em] &= -\frac{1}{g'(x)}(w(x,g(x))-w(g(x),x)g'(x)) \\[1em] &= -\frac{1}{g'(x)}\exp(\bar{u}(x)) \end{align*} for almost all $x \in [0,1]$. Since $g$, $g'$ and $\bar{u}$ are continuous we have \begin{align} \exp(\bar{u}(x)) = -g'(x)\exp(\bar{u}(g(x))) \tag{5} \end{align} for all $x \in [0,1]$. $$\tag*{$\Box$}$$

Claim 2. If

(i) $\bar{u}$ is the solution of $(1)$

(ii) $\bar{u} \in C^1[0,1]$

(iii) there exists $g \in C^2[0,1]$ such that $$\{(x,g(x)) : x \in [0,1]\} = \left\{(x,y) \in S : I(\bar{u})(x,y) = 0\right\}$$ and $$\{(x,g(x)) : x \in (0,1)\} \subseteq \operatorname{int}(S),$$ then $$g(x) = 1+\sqrt{2}+x-\sqrt{4 \left(1+\sqrt{2}\right) x+2},$$ and $$\exp(\bar{u}(x)) = \sqrt{2 \left(1+\sqrt{2}\right)}-\sqrt{2 x+\sqrt{2}-1}.$$

Proof. Let $x \in (0,1)$. We have $I(\bar{u})(x,g(x)) = 0$. Since $I(\bar{u}) \geq 0$, we have that $(x,g(x))$ is a minimum point of $I(\bar{u})$. Since $I(\bar{u})$ is a $C^1$-function by $(ii)$, we have that $I(\bar{u})'(x,g(x)) = 0$. Therefore \begin{align} \bar{u}'(x) = -\frac{1}{2-x-g(x)}. \tag{6} \end{align} By Claim 1 we have $(5)$. We will see that $(5)$ and $(6)$ determine $g$ and $\bar{u}$ uniquely. The following calculations hold for all $x \in [0,1]$.

Since $I(\bar{u})(x,g(x)) = 0$, we have \begin{align*} \bar{u}(g(x)) = \log(2-x-g(x)) - \bar{u}(x), \end{align*} and thus with $(5)$ we have \begin{align} \bar{u}(x) = \frac{1}{2}\left(\log(-g'(x)) + \log(2-x-g(x))\right), \tag{7} \end{align} and thus \begin{align} \bar{u}'(x) = \frac{1}{2}\left(\frac{g''(x)}{g'(x)} + \frac{-1-g'(x)}{2-x-g(x)}\right). \tag{8} \end{align} Putting $(6)$ and $(8)$ together yields $$g''(x)(2-x-g(x)) -g'(x)^2 +g'(x) = 0.$$ Therefore \begin{align} g'(x)(2-x-g(x)) +2g(x) = a. \tag{9} \end{align} for some $a \in \mathbb{R}$. In particular, we have \begin{align} g'(0)(2-g(0)) +2g(0)= g'(1)(1-g(1)) +2g(1). \tag{10} \end{align} Since $g$ is an involution we have $g(0) = 1$, $g(1) = 0$, $1 = g'(g(0))g'(0)= g'(1)g'(0)$ and $g' < 0$. We put this into $(10)$ and get $a = 1-\sqrt{2}$. Thus \begin{align} g'(x) = \frac{1-\sqrt{2}-2g(x)}{2-x-g(x)}. \tag{11} \end{align} Now we replace $x$ with $g(x)$ in $(9)$ and then use $g'(g(x)) = \frac{1}{g'(x)}$. We get \begin{align} g'(x) = \frac{2-x-g(x)}{1-\sqrt{2}-2x}. \tag{12} \end{align} Putting $(11)$ and $(12)$ together yields a quadratic equation for $g(x)$. Only the solution \begin{align} g(x) = 1+\sqrt{2}+x-\sqrt{4 \left(1+\sqrt{2}\right) x+2} \tag{13} \end{align} satisfies $g(0)=1$. We also have \begin{align*} \exp(\bar{u}(g(x)))^2 &\underset{\hphantom{(12)}}{=} \frac{2-x-g(x)}{\exp(\bar{u}(x))}\exp(\bar{u}(g(x))) \\[1em] &\underset{(5)\hphantom{0}}{=} -\frac{2-x-g(x)}{g'(x)} \\[1em] &\underset{(12)}{=} 2 x+\sqrt{2}-1, \end{align*} and thus \begin{align*} \exp(\bar{u}(x)) &\underset{\hphantom{(12)}}{=} \frac{2-x-g(x)}{\sqrt{2 x+\sqrt{2}-1}} \\[1em] &\underset{(13)}{=} \frac{1-2x-\sqrt{2}+\sqrt{4 \left(1+\sqrt{2}\right) x+2}}{\sqrt{2 x+\sqrt{2}-1}} \\[1em] &\underset{\hphantom{(12)}}{=} -\sqrt{2 x+\sqrt{2}-1}+\frac{\sqrt{4 \left(1+\sqrt{2}\right) x+2}}{\sqrt{2 x+\sqrt{2}-1}} \\[1em] &\underset{\hphantom{(12)}}{=} -\sqrt{2 x+\sqrt{2}-1}+\sqrt{2 \left(1+\sqrt{2}\right)}. \end{align*} $$\tag*{$\Box$}$$

We define \begin{align*} \bar{u} : [0,1] \rightarrow \mathbb{R}, \quad \bar{u}(x) &:= \log\left(\sqrt{2 \left(1+\sqrt{2}\right)}-\sqrt{2 x+\sqrt{2}-1}\right), \\[1em]g : [0,1] \rightarrow [0,1], \quad g(x) &:= 1+\sqrt{2}+x-\sqrt{4 \left(1+\sqrt{2}\right) x+2}. \end{align*}

Claim 3. $g$ is an involution. We have \begin{align*} I(\bar{u})(x,g(x)) &= 0, \\[0.5em] \exp(\bar{u}(x) + \bar{u}(y)) &\geq 2-x-y \end{align*} for all $x,y \in [0,1]^2$, and thus $I(\bar{u}) \geq 0$.

Proof. We solve $g(x)=y$ for $x$ and see that $x=g(y)$. Thus $g(g(x))=x$ and $g$ is an involution on $[0,1]$. We define $$F : [0,1]^2 \rightarrow \mathbb{R}, \quad F(x,y) := \exp(\bar{u}(x)+\bar{u}(y)) - (2-x-y).$$ For all $x \in [0,1]$ we have $x + g(x) \leq 1$ and thus $(x,g(x)) \in S$. We see that $\exp(\bar{u}(x))^2 = 2 g(x)+\sqrt{2}-1$, thus $\exp(\bar{u}(g(x)))^2 = 2 x+\sqrt{2}-1$ and by putting this into $F(x,g(x))$ we get $F(x,g(x)) = 0$ and $I(\bar{u})(x,g(x)) = 0$. For all $y \in [0,1]$ we have
\begin{align*} (\partial_{y y} F)(x,y) &= \exp(\bar{u}(x))\, \partial_{y y} \exp(\bar{u}(y)) \\ &= \exp(\bar{u}(x))\, \frac{1}{\left(2 y+\sqrt{2}-1\right)^{3/2}} \\ &> 0. \end{align*} Therefore $y \mapsto F(x,y)$ is convex and since $(\partial_y F)(x,g(x))= 0$, we have that $(x,g(x))$ is the global minimizer of $y \mapsto F(x,y)$. Since $F(x,g(x)) = 0$ we have $F \geq 0$ and thus $I(\bar{u}) \geq 0$. $$\tag*{$\Box$}$$

Claim 4. $\bar{u}$ is the unique solution of $(1)$.

Proof. We define \begin{alignat*}{2} &w : [0,1] \rightarrow [0,\infty), \quad &&w(x) := \frac{\exp(\bar{u}(x))}{1-g'(x)}, \\[1em] &\psi : C(S) \rightarrow \mathbb{R}, \quad &&\psi(v) := \int_0^1 v(x,g(x)) \, w(x) \, \mathrm{d}x, \\[1em] &L : C[0,1] \rightarrow \mathbb{R}, \quad &&L(u) := J(u) - \psi(I(u)). \end{alignat*} $w$ is well-defined since $g$ being an involution and not the identity implies $g'\leq0$.

$\psi$ is well-defined since $(x,g(x)) \in S$ for all $x \in [0,1]$. We have $w(g(x))=w(x)$ and thus \begin{align*} L'(\bar{u})(h) &= J'(\bar{u})(h) - \psi'(I(\bar{u}))(I'(h)) \\[1em] &= J'(\bar{u})(h) - \psi(I'(h)) \\[1em] &= \int_0^1 \exp(\bar{u}(x))\, h(x) \, \mathrm{d}x - \int_0^1 (h(x)+h(g(x))) \, w(x) \, \mathrm{d}x \\[1em] \text{by substitution:} \\[0.5em] &= \int_0^1 \exp(\bar{u}(x))\, h(x) \, \mathrm{d}x - \int_0^1 h(x) \, (1-g'(x)) \,w(x)\, \mathrm{d}x \\[1em] &= \int_0^1 \exp(\bar{u}(x))\, h(x) \, \mathrm{d}x - \int_0^1 \exp(\bar{u}(x)) \, h(x) \, \mathrm{d}x \\[1em] &= 0. \end{align*} for all $h \in C[0,1]$. Since $J$ and $-(\psi \circ I)$ are convex, $L$ is convex. We have $L'(\bar{u})=0$ and thus $\bar{u}$ is a global minimizer of $L$. Since $\psi$ is a positive functional, we have $L(u) \leq J(u)$ for all $u \in C[0,1]$ with $I(u) \geq 0$. But $\psi(I(\bar{u}))= 0$ since $I(\bar{u})(x,g(x))=0$ by Claim 3 for all $x \in [0,1]$. Therefore $L(\bar{u})=J(\bar{u})$ and thus $J(\bar{u}) \leq J(u)$ for all $u \in C[0,1]$ with $I(u) \geq 0$. By Claim 3 we have $I(\bar{u}) \geq 0$. Therefore $\bar{u}$ is a solution of $(1)$.

Assume there is a $\tilde{u} \in C[0,1]$ such that $I(\tilde{u}) \geq 0$ and $J(\tilde{u}) \leq J(\bar{u})$. We set $$\widehat{u} := \frac{\tilde{u} + \bar{u}}{2}.$$ We have $I(\widehat{u})\geq 0$. Since $J$ is strictly convex, $\bar{u} = \widehat{u} = \tilde{u}$. Therefore $\bar{u}$ is the unique solution of $(1)$. $$\tag*{$\Box$}$$

Claim 5. The unique solution of $(2)$ is given by $$\bar{f}(x)= \begin{cases} \dfrac{\exp(\bar{u}(2x))}{\sqrt{2}}&\text{if}\quad 0 \leq x \leq \frac{1}{2},\\ \dfrac{\exp(\bar{u}(2(1-x)))}{\sqrt{2}}&\text{if}\quad \frac{1}{2} < x \leq 1. \end{cases}$$

Proof. Since $\exp > 0$, we have $\bar{f} > 0$. Let $x,y \in[0,1]$ such that $x \leq y$.

If $x \leq \frac{1}{2} \leq y$, then \begin{align} \bar{f}(x)\bar{f}(y)&=\frac{1}{2}\exp\left(\bar{u}(2x)+\bar{u}(2(1-y))\right) \nonumber \\ &\geq \frac{1}{2}(2- 2x - 2(1-y)) \qquad \text{(by Claim 3)} \nonumber \\ &=y-x \tag{14} \\ &= |x-y|. \nonumber \end{align} If $x \leq y \leq \frac{1}{2}$, then $$\bar{f}(x)\bar{f}(y)=\bar{f}(x)\bar{f}(1-y) \underset{(14)}{\geq} 1-y-x \geq y-x = |x-y|.$$ If $\frac{1}{2} \leq x \leq y$, then $$\bar{f}(x)\bar{f}(y)=\bar{f}(1-x)\bar{f}(y) \underset{(14)}{\geq} y-(1-x) \geq y-x = |x-y|.$$ Thus $\bar{f}(x)\bar{f}(y) \geq |x-y|$ for all $x,y \in [0,1]$.

Assume there exists $\tilde{f}$ such that $\tilde{f}$ satisfies the constraints of (2) and $$\int_0^1 \tilde{f} \, \mathrm{d}x \leq \int_0^1 \bar{f} \, \mathrm{d}x.$$ We set $$\widehat{f}(x):= \left(\tilde{f}(x)\tilde{f}(1-x)\bar{f}(x)^2\right)^\frac{1}{4}.$$ $\widehat{f}$ satisfies the constraints of (2) and \begin{align} \int_0^1 \widehat{f}(x) \, \mathrm{d}x &= \int_0^1 \left(\tilde{f}(x)\tilde{f}(1-x)\bar{f}(x)^2\right)^\frac{1}{4} \, \mathrm{d}x \nonumber \\[1em] &\leq \int_0^1 \frac{\tilde{f}(x)+\tilde{f}(1-x)+2\bar{f}(1-x)}{4} \, \mathrm{d}x \tag{15} \\[1em] &= \int_0^1 \frac{\tilde{f}(x)+\bar{f}(x)}{2} \, \mathrm{d}x \nonumber \\[1em] &\leq \int_0^1 \bar{f}(x) \, \mathrm{d}x. \nonumber \end{align} Since $\widehat{f}(x) = \widehat{f}(1-x)$ and $\bar{f}(x) = \bar{f}(1-x)$ for all $x \in [0,1]$, we thus have \begin{align} \int_0^{\frac{1}{2}} \widehat{f}(x) \, \mathrm{d}x \leq \int_0^{\frac{1}{2}} \bar{f}(x) \, \mathrm{d}x. \tag{16} \end{align} We set $$\widehat{u}(x) := \log\left(\sqrt{2}\, \widehat{f}\left(\frac{x}{2}\right)\right),$$ and by $(16)$ we have $J(\widehat{u}) \leq J(\bar{u})$. We also have $I(\widehat{u}) \geq 0$ since \begin{align*} \exp(\widehat{u}(x)+\widehat{u}(y)) &= 2\widehat{f}\left(\frac{x}{2}\right)\widehat{f}\left(\frac{y}{2}\right) \\[1em] &= 2\widehat{f}\left(\frac{x}{2}\right)\widehat{f}\left(1-\frac{y}{2}\right) \\[1em] &\geq 2\left|1-\frac{x}{2}-\frac{y}{2}\right| \\[1em] &= 2-x-y \end{align*} for all $x,y \in [0,1]$. By Claim 4, $\widehat{u} = \bar{u}$. Since $$\widehat{f}(x)=\frac{\exp(\widehat{u}(2x))}{\sqrt{2}}$$ for all $x \in [0,\frac{1}{2}]$ by definition of $\widehat{u}$, we have $\widehat{f} = \bar{f}$. The inequality at $(15)$ must be an equality and thus $\tilde{f} = \widehat{f} = \bar{f}$. Therefore $\bar{f}$ is the unique solution of $(2)$. $$\tag*{$\Box$}$$

Answer 5

Extending kimchi lover's idea:

$$I = n \int_0^{1/n} \frac{1}{n} \sum_{k=0}^{n-1} f(x+k/n) dx \geq n \int_0^{1/n} \left(\prod_{k=0}^{n-1} f(x+k/n) \right)^{1/n} dx$$

Pairing up opposite edges, then we can pick pairs $(x+k/n, x+(n-k+1)/n)$, with $n=2m$, such that

$$\lim_{n \to \infty} I \geq \lim_{n \to \infty} 2m \int_0^{1/2m} \left( \prod_{k=1}^{m} \left(\frac{2k-1}{2m} \right) \right)^{1/2m} dx = \lim_{m \to \infty} \frac{[(2m-1)!!]^{1/2m}}{(2m)^{1/2}} = \sqrt{\frac{1}{e}}$$

where we compute the limit using wolfram alpha.

This bound isn't the best one found so far, but perhaps my approach will be inspiring. Loved thinking about the problem!

EDIT: More information. Using a continuous approximate (from above) to the step function $f(x)=a^{1/2} \chi_{[0,a]} + a^{-1/2} \chi_{(a,1]}$, you should be able to obtain a value below 1 for the integral if I did by calculation correctly. It is clear that $f=1$ means the minimum is less than or equal to 1.