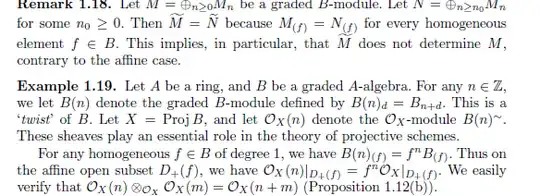Let $\mathcal {O}(-1)$ be the tautological line bundle $X$ of $ \Bbb CP^1$, where $X=\{(z,l) \in \Bbb C^2 \times \Bbb CP^1 : z \in l \}$ together with canonical projection $X \to \Bbb CP^1$ (line bundle property and co easy to prove).
Futhermore we define $ \mathcal {O}(1):= \mathcal {O}(-1)^{\vee}$, where $ \mathcal {O}(-1)^{\vee}$ can be defined in two equivalent ways :
$ \mathcal {O}(-1) \otimes \mathcal {O}(-1)^{\vee}= \mathcal {O}_{\Bbb CP^1}$ is the same as to define it as $ \mathcal {O}(-1)^V := \underline{Hom}_{\mathcal{O}_{\Bbb CP^1}}(\mathcal{O}(-1),\mathcal{O}_{\Bbb CP^1})$ (follows from evaluation map).
The other way to define $ \mathcal {O}(1)$ is the following (compare with eg Liu’s AG, page 165 or see image below):
Obviously we have $ \Bbb CP^1 = Proj (B)$ where $B = \oplus _n B_n:=\mathbb{C}[X,Y] $ is graded $\mathbb{C}$-algebra in canonical way (polynomial grade). We set $B(n)$ as a new graduated $\mathbb{C}$-algebra by defining recursively $B(n)_m := B_{n+m}$. Liu defined the $ \mathcal {O}_{\Bbb CP^1 }$ -module $ \mathcal {O}(n)$ by setting $ \mathcal {O}(n) := \widetilde{B(n)}$ .
My question is: Why this both definitions of $ \mathcal {O}(1)$ are equivalent?
Here Liu's definition of "twisting":