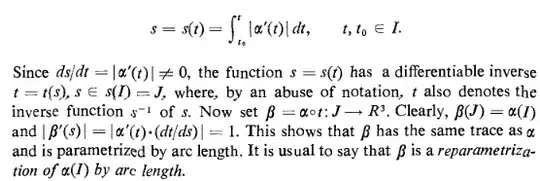The trace of the parametrized curve is
$$\alpha(t)=(t,\cosh t),\ t\in\mathbb R$$
is called catenary.
I want to show the curvature of the catenary is
$$k(t)=\frac{1}{\cosh^2t}$$
Before finding the curvature I need to parametrize it by arc length. Do Carmo in his classical Differential Geometry book makes the following remark about it on page 22:
since the catenary is defined for every $t\in \mathbb R$, I'm having trouble to know the value of $t_0$, can it be anything?