How to approximate relative error further?

Question

Background and original problem:

I want to minimize the difference (error) of a numerical derivative approximation of a function and its true derivative.

Let $f(x) = \sin(x) $ be the anti-derivative of $f'(x)$ and $\delta_h f$ be the approximated differentiation ($\Delta y / \Delta x$) and let $x=2$ for both cases.

I calculate now the difference between the two, and decrease the $\Delta x$ so I will get a better approximation of the derivative at that point.

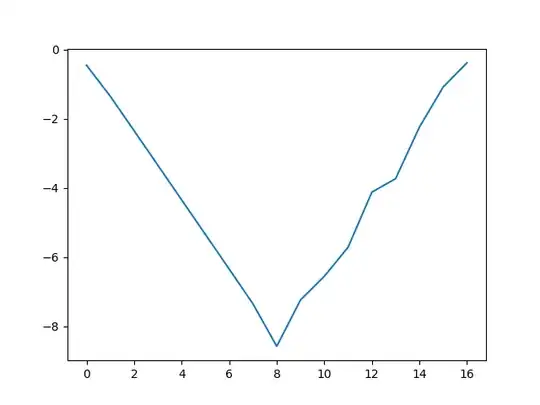
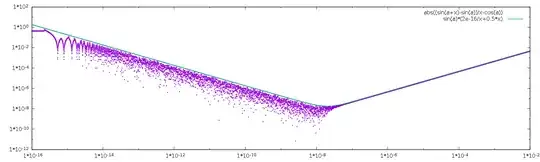
So I plot my difference $ \log_{10}|f' - \delta_h f|$ and the result is the following.

At first it is falling because that's what you'd expect it to do, due to the rising precision of the approximation. Then it rises, presumably due to various rounding errors that happen during the approximation, whereas in the true derivative of $f(x)$ our rounding error is in the margin of error of our machine epsilon, so the increase in error is definitely caused by our approximation and the rounding errors in it.

This is how $f'(x)$ and $\delta_h f $ are defined:

$$f'(x) = \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h) $$ where $\mathcal{O}(h)$ is the magnitude of our machine eps.

$$\delta_h f = \frac{f(x+h) - f(x)}{h} $$

$ h = 10^{-1*k} k \in N $ where k increases with each step on the plot.

Given these formulae we can give the resulting relative error:

$| \mathcal{O}(h) - \frac{f(x+h)}{h}\delta | $

But I don't know any further than this.

I also want to be able to explain how the rounding error of the $\Delta x$ has its effect on the total error.

My exact question is: How can I further formalize and understand the effect of the rounding errors, specifically the subtraction error in the approximation ?

I have tried and got stuck at the above point.

Answer 1

You got some of the details right. The error of the difference quotient is in first order $\frac12f''(x)h+O(h^2)$. The combined error of the sine evaluations is bounded by $|f(x)|δ$ if $δ\approx 2\cdot 10^{-16}$ is the floating point machine constant. In total you get an error bound of $$ \frac{|f(x)|δ}{h}+\frac12|f''(x)|h+O(h^2) $$ As for $f(x)=\sin(x)$ you get $f''(x)=-\sin(x)$, the minimum of this error bound can be found by minimizing $\fracδh+\frac h2$ which is at $h=\sqrt{2δ}=2⋅10^{-8}$.

The correctness of this bound and its minimum can be seen if you sample the formula at some more points and graph them together with the bound,

---

A general heuristic is that with an order $p$ approximation of the $k^{\rm th}$ derivative you get error terms $O(h^p)$ from the method itself and $O(δ/h^k)$ from the floating point evaluation. The overall error is lowest when both terms are about equal, that is at $$ h=\sqrt[p+k\,]δ $$ which gives the somewhat counter-intuitive rule that the higher these numbers the larger the optimal $h$.