First note that if $u=U-x\sin \left( t \right)$ , then we have the following ${{u}_{tt}}={{U}_{tt}}+x\sin \left( t \right),\,\,\,\,{{u}_{xx}}={{U}_{xx}}$ so
$${{u}_{tt}}-{{u}_{xx}}-x\sin \left( t \right)=0\Rightarrow {{U}_{tt}}-{{U}_{xx}}=0$$
The PDE and boundary conditions therefore become
${{U}_{tt}}\left( x,t \right)-{{U}_{xx}}\left( x,t \right)=0$ , $U\left( x,0 \right)=x\left( x-1 \right)$,${{U}_{t}}\left( x,0 \right)=x$, $U\left( 0,t \right)=0$, $U\left( 1,t \right)=\sin \left( t \right)$
It is clear now that the system is equivalent to a wave being driven from the right most boundary. Now take the Laplace transform
$$-{{U}_{t}}\left( x,0 \right)-sU\left( x,0 \right)+{{s}^{2}}U\left( x,s \right)-{{U}_{xx}}\left( x,s \right)=0$$
Substituting the initial conditions $U\left( x,0 \right)=x\left( x-1 \right)$,${{U}_{t}}\left( x,0 \right)=x$ we have
$${{U}_{xx}}\left( x,s \right)-{{s}^{2}}U\left( x,s \right)+x+sx\left( x-1 \right)=0$$
Now the remaining boundary conditions when transformed become
$U\left( 0,s \right)=0$, $U\left( 1,s \right)=\frac{1}{1+{{s}^{2}}}$
We therefore have a second order ODE with two BCs. Solving this equation using the method of undetermined coefficients we find
$$U\left( x,s \right)=A{{e}^{-sx}}+B{{e}^{sx}}+\frac{1}{{{s}^{3}}}\left( 2+\left( x-1 \right)x{{s}^{2}}+sx \right)$$
Applying the boundary conditions we find therefore
$$U\left( x,s \right)=\frac{2\left( {{s}^{2}}+1 \right){{e}^{s}}-2{{s}^{2}}-s-2}{{{s}^{3}}\left( {{s}^{2}}+1 \right)\left( {{e}^{-s}}-{{e}^{s}} \right)}{{e}^{-sx}}-\frac{2\left( {{s}^{2}}+1 \right){{e}^{-s}}-2{{s}^{2}}-s-2}{{{s}^{3}}\left( {{s}^{2}}+1 \right)\left( {{e}^{-s}}-{{e}^{s}} \right)}{{e}^{sx}}+\frac{1}{{{s}^{3}}}\left( 2+\left( x-1 \right)x{{s}^{2}}+sx \right)$$
This may be written as
$$U\left( x,s \right)=\frac{2\sinh \left( \left( x-1 \right)s \right)}{{{s}^{3}}\sinh \left( s \right)}-\frac{2}{{{s}^{3}}}\left( 1+\frac{s}{2\left( {{s}^{2}}+1 \right)} \right)\frac{\sinh \left( sx \right)}{\sinh \left( s \right)}+\frac{1}{{{s}^{3}}}\left( 2+\left( x-1 \right)x{{s}^{2}}+sx \right)$$
The solution therefore is given by
$$\begin{align}
& U\left( x,t \right)=\frac{1}{2\pi i}\int\limits_{c-i\infty }^{c+i\infty }{\frac{2}{{{s}^{3}}}\frac{\sinh \left( \left( x-1 \right)s \right)}{\sinh \left( s \right)}{{e}^{ts}}-\frac{2}{{{s}^{3}}}\left( 1+\frac{s}{2\left( {{s}^{2}}+1 \right)} \right)\frac{\sinh \left( sx \right)}{\sinh \left( s \right)}{{e}^{ts}}+\frac{1}{{{s}^{3}}}\left( 2+\left( x-1 \right)x{{s}^{2}}+sx \right){{e}^{ts}}ds} \\
& ={{I}_{1}}-{{I}_{2}}+{{I}_{3}} \\
\end{align}$$
Where the labelling/grouping of integrals is according to the grouping of coefficients of ${{e}^{ts}}$. The line of integration must be taken so all poles are to its left. We will consider a closed contour consisting of a straight line segment $\left[ c-iR,c+iR \right]$ where c,R>0, which is closed by a half circle to either the left or right of the line. The poles of all the integrals exist along the imaginary axis at $s=0,s=\pm i,s=n\pi i$, hence if we close the contour to the left then, for example, ${{I}_{1}}=\sum\limits_{{}}{res}$ , i.e. the sum of the residues of the integrand. If, however, we close the contour to the right, then the contour will enclose no poles and hence ${{I}_{1}}=0$. We will use the same type of contour for the other two integrals and so the same may be said of them as well. Observe that ${{I}_{3}}\sim {{e}^{st}},\,\,\left| s \right|\to \infty $ and so for the integral along the circular contour to vanish we must have either t>0 and close to the left or t<0 and close to the right. The latter is not physical and so we close to the left.
Now consider the limit of $\left| s \right|\to \infty $ for the first two integrals. Let $s=R\cos \left( \theta \right)+iR\sin \left( \theta \right)$ then effectively the conditions for the circular contour integrals to become zero as $R\to \infty $, for ${{I}_{1}}$and ${{I}_{2}}$ respectively are
$${{e}^{\left( t+x \right)R\cos \left( \theta \right)}}-{{e}^{-\left( x-t-2 \right)R\cos \left( \theta \right)}},R\cos \left( \theta \right)<0\Rightarrow t+x>0\cap \,\,x-t-2<0$$
$${{e}^{\left( x+t+1 \right)R\cos \left( \theta \right)}}-{{e}^{-(x-t-1)R\cos \left( \theta \right)}},\,\,\,R\cos \left( \theta \right)<0\Rightarrow \,\,\,x+t>-1\cap \,x-1<t$$
Both conditions are satisfied for all x and t since $0\le x\le 1$ and $t\ge 0$ . To make calculations more tractable consider the residues of each integral separately, and so define
${{k}_{1}}\left( s \right)=\frac{2}{{{s}^{3}}}\frac{\sinh \left( \left( x-1 \right)s \right)}{\sinh \left( s \right)}{{e}^{ts}}$, ${{k}_{2}}\left( s \right)=\frac{2}{{{s}^{3}}}\left( 1+\frac{s}{2\left( {{s}^{2}}+1 \right)} \right)\frac{\sinh \left( sx \right)}{\sinh \left( s \right)}{{e}^{ts}}$ and ${{k}_{3}}\left( s \right)=\frac{1}{{{s}^{3}}}\left( 2+\left( x-1 \right)x{{s}^{2}}+sx \right){{e}^{ts}}$
We have then
$$\underset{s=0}{\mathop{res}}\,{{k}_{1}}\left( s \right)=\frac{1}{3}\left( x-1 \right)\left( 3{{t}^{2}}+x\left( x-2 \right) \right)$$
$$\underset{s=0}{\mathop{res}}\,{{k}_{2}}\left( s \right)=\frac{1}{3}\left( 3t\left( x+t \right)+x\left( {{x}^{2}}-1 \right) \right)$$
$$\underset{s=0}{\mathop{res}}\,{{k}_{3}}\left( s \right)=t\left( t+x \right)+x\left( x-1 \right)$$
(note that $\underset{s=0}{\mathop{res}}\,{{k}_{1}}\left( s \right)-{{k}_{2}}\left( s \right)+{{k}_{3}}\left( s \right)=0$)
$$\sum{\underset{s=\pm i}{\mathop{res}}\,{{k}_{2}}\left( s \right)}=-\frac{\sin \left( t \right)\sin \left( x \right)}{\sin \left( 1 \right)}$$
$$\sum\limits_{n'=-\infty }^{\infty }{\underset{s=n\pi i}{\mathop{res}}\,{{k}_{1}}\left( s \right)}=\sum\limits_{n'=-\infty }^{\infty }{{{\left( -1 \right)}^{n}}}\frac{2\sinh \left( \left( x-1 \right)in\pi \right)}{-i{{n}^{3}}{{\pi }^{3}}}{{e}^{in\pi t}}$$
$$\sum\limits_{n'=-\infty }^{\infty }{\underset{s=n\pi i}{\mathop{res}}\,{{k}_{2}}\left( s \right)}=\sum\limits_{n'=-\infty }^{\infty }{{{\left( -1 \right)}^{n}}\frac{2}{-i{{n}^{3}}{{\pi }^{3}}}\left( 1+\frac{in\pi }{\left( 1-{{n}^{2}}{{\pi }^{2}} \right)} \right)\sinh \left( in\pi x \right){{e}^{in\pi t}}}$$
Where the dash on the summation implies $n=0$ is omitted. The last set of residues may be written as
$$\sum\limits_{n'=-\infty }^{\infty }{\underset{s=n\pi i}{\mathop{res}}\,{{k}_{1}}\left( s \right)}=-\sum\limits_{n=1}^{\infty }{\frac{4\sin \left( xn\pi \right)\cos \left( n\pi t \right)}{{{n}^{3}}{{\pi }^{3}}}}$$
$$\sum\limits_{n'=-\infty }^{\infty }{\underset{s=n\pi i}{\mathop{res}}\,{{k}_{2}}\left( s \right)}=\sum\limits_{n=1}^{\infty }{{{\left( -1 \right)}^{n+1}}\frac{2\sin \left( n\pi x \right)}{{{n}^{3}}{{\pi }^{3}}}\left( 2\cos \left( n\pi t \right)+\frac{2n\pi \sin \left( n\pi t \right)}{\left( {{n}^{2}}{{\pi }^{2}}-1 \right)} \right)}$$
Finally we have therefore
$$U\left( x,t \right)=\frac{\sin \left( t \right)\sin \left( x \right)}{\sin \left( 1 \right)}+\sum\limits_{n=1}^{\infty }{\frac{4\sin \left( n\pi x \right)}{{{n}^{3}}{{\pi }^{3}}}\left( \left( {{\left( -1 \right)}^{n}}-1 \right)\cos \left( n\pi t \right)+{{\left( -1 \right)}^{n}}\frac{n\pi \sin \left( n\pi t \right)}{\left( {{n}^{2}}{{\pi }^{2}}-1 \right)} \right)}$$
While we should now proceed to check that this solution satisfies all conditions (which is easiest from the contour representation), for now (for me anyway) it will suffice to compare it to a numerical solution from Maple to make sure i havent dropped terms or done something stupid.
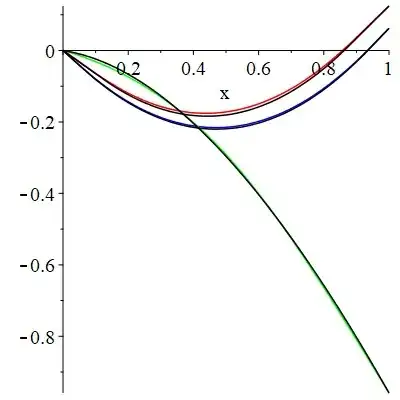
The colour plots are Maple’s numerical solution of the system, while the black plots are the ‘exact’ solution taken to n=200. They are for t=1/16 (blue) t=1/8 (red) t=5 (green). A table of numerical values for comparison would probably be more useful, but my knowledge of maple isn't fantastic and so i can't really comment as to the accuracy (or how to improve it) of the numerical solution. What it suggests to me, however, is that i probably haven't dropped a term or some other typo since both solutions appear to very similar. I strongly urge you to verify the entire calculation since some of the algebra gets quite thick in places.
