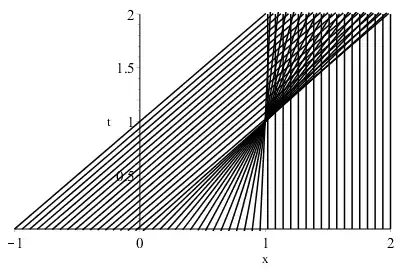
In this notes, example 5, page 5. It gives an example on how to solve a PDE where characteristics might cross using the Rankine-Hugoniot condition. The example is in an initial-value problem for Burgers' equation $u_t + u u_x = 0$, with piecewise linear initial data $$ u(x,0) = \phi(x) = \left\lbrace\begin{aligned} &1 &&\text{if}\quad x<0\\ &1-x &&\text{if}\quad 0<x<1\\ &0 &&\text{if}\quad 1<x \end{aligned}\right. $$ I have two questions about it:
1). In my opinion, Rankine-Hugoniot condition is just a necessary condition for the discontinuous points of a solution. How does it guarantee the thing we get is indeed a solution?
2).Using the Rankine-Hugoniot condition we can only calculate the speed of the curve of discontinuities. How do we locate its exact formula?(i.e. how to choose one-point on it). Can we choose any arbitrary point where the characteristics cross?