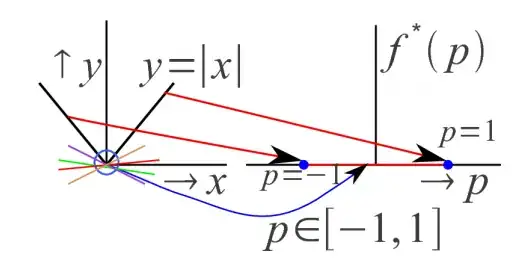
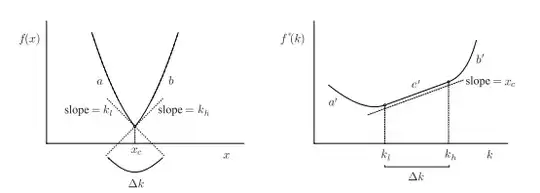
I gathered different handouts from the internet and tried to figure out what fenchel transformation was, but I stumbled on two different results of fenchel transformation of $f(x) = |x|$:
First results is:
Second result is:
I believe the first one is correct but can anyone confirm this for me? In addition, should there be vertical lines at $p=-1$ and $p=1$?