2

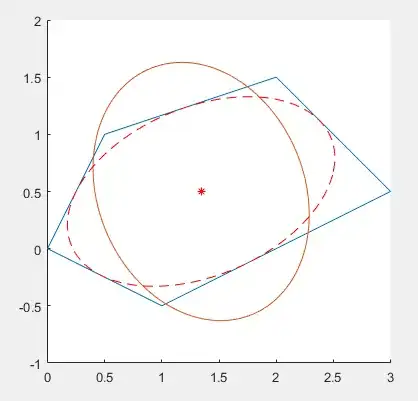
I am trying to use the CVX package in Matlab to find the largest inscribed ellipsoid for a convex set of points. I was also able to get the example from this link running.

[Step 1] This is how the optimization problem is formulated in the sample Matlab code: 

% formulate and solve the problem  
cvx_begin  
    variable B(n,n) symmetric  
    variable d(n)  
    maximize( det_rootn( B ) )  
    subject to  
       for i = 1:m  
           norm( B*A(i,:)', 2 ) + A(i,:)*d <= b(i);  
       end
cvx_end

[Step 2] To plot the inner ellipsoid the sample MATLAB code suggests:

% make the plots
noangles = 200;
angles   = linspace( 0, 2 * pi, noangles );
ellipse_inner  = B * [ cos(angles) ; sin(angles) ] + d * ones(1, noangles);
plot( ellipse_inner(1,:), ellipse_inner(2,:), 'r--' );

My question is, how can I change the formulation in [Step 1] so that the ellipsoid matrix 'B' directly captures the orientation and shape of the inscribed ellipsoid without requiring (what I think is) an affine transformation from step [Step 2]?

As of now, if I plot an ellipsoid using the variable 'B' directly (using the Ellipse_plot tool from Matlab File Exchange), it is not aligned with the convex polygon! Misaligned ellipsoid image link

Rodrigo de Azevedo
  • 23,223
optimum_Jay
  • 68

1 Answers1

3

$B$ is not the matrix $Q$ in a form $(x-d)^TQ^{-1}(x-d)\leq 1$ but a factor of it. This transformation (or something similiar) is required to arrive at a convex problem.

You want $a^Tx \leq b$ for all $(x-d)^TQ^{-1}(x-d)\leq 1$ which is equivalent to $a^T(z+d) \leq b$ for all $z^TQ^{-1}z\leq 1$ which is equivalent to $a^T(B^Ty+d) \leq b$ for all $y^Ty\leq 1$ where $Q = BB^T$. Now maximize over $y$ and the constraint ends up at $\||Ba\|| + a^Td \leq b$

Johan Löfberg
  • 9,737
  • 1
  • 16
  • 15
  • Thank you so much for the prompt answer @Johan! :) So just to be clear, I understand I should read the final equivalent statement as: a^T(B^T y + d) ≤ b for all y^T (B * Q^-1 * B^T) y = y^T y ≤ 1 and this happens since Q = BB^T where B is symmetric. Also, after reading your statement that B is actually a Cholesky factor, I was able to obtain the ellipsoid matrix equation as inv(B*B') which I plotted in matlab as: https://imgur.com/a/rc2LM – optimum_Jay Oct 05 '17 at 02:37
  • However, I did not understand the part where you suggest I maximise over 'y' - As in 'y' is not present in the constraint equation |∥Ba∥| + a^T d ≤ b anywhere! - Also, maybe I am stating something that is obvious but I am a bit surprised I was able to obtain the ellipsoid matrix form just by performing inv(B*B') and not modifying the existing optimization formulation at all! Could you please clarify these two points? Again, thank you so much for your time! :) – optimum_Jay Oct 05 '17 at 02:54
  • After two coordinate changes, we have a linear constrant in y. You then want $a^T(B^Ty+d) \leq b ~\forall y^Ty\leq 1$. The maximal value $y^T(Ba)$ can achieve when $y^Ty\leq 1$ is $|Ba|$ (by selecting $y$ parallell to $Ba$ and scale it to have unit length). The final result is a second-order cone constraint in the decision variables $B$ and $d$. The variable of interest, $Q$, is computed after the problem has been solved. – Johan Löfberg Oct 05 '17 at 06:15
  • Okay now I understand. A final question, I was under the impression that Cholesky factors are always in the lower-upper form. However, this does not seem to be the case with B which in my case is symmetric. How does this work? – optimum_Jay Oct 05 '17 at 09:15
  • I shouldn't have said Cholesky factor. It's a factor such that $Q=BB^T$. Cholesky is one example. Changed this in answer – Johan Löfberg Oct 05 '17 at 13:10