Periodic orbit of differential equation

Question

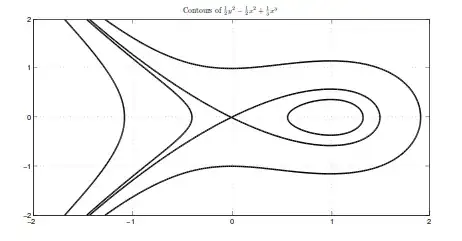
Let $f(t,x,y)$ be the flow given by the system $$\dot{x}=y\qquad\dot{y}=x-x^2$$ and $O(x,y)$ the orbit starting at initial condition $(x,y)$.

Let $P$ be the set of initial conditions $(x,y)$ such that $O(x,y)$ is periodic.

Let $A_+$ be the set of initial conditions $(x,y)$ such that the limit of $t\rightarrow \infty$ of $O_+(x,y)$ exists.

Let $A_-$ be the set of initial conditions $(x,y)$ such that the limit of $t\rightarrow -\infty$ of $O_-(x,y)$ exists.

Let $A$ be the set of initial conditions $(x,y)$ such that the limits of $t\rightarrow \infty$ and $t\rightarrow -\infty$ of $O(x,y)$ exist.

How to find $P$, $A_+$, $A_-$ and $A$?

What I thought:

The orbit $O(x,y)$ is given by $\{f(t,x,y):t\in\mathbb{R}\}$, where $O_+$ means that we restrict $t\geq 0$ and $O_-$ that $t\leq0$.

I know what the Hamiltonian is and what the Jacobian is of the system, but I just cannot see what my next step should be. Could someone point me in the right direction?

Here is the phase portrait:

@mercio Do you mean a phase portrait? Because I have one, and I can see which should be the sets. But I don't know how to find them exactly — Siegfried Bernthaller, Oct 03 '17 at 10:03
you could even draw $A_+,A_-$ and $P$. What do you mean by "finding them" ? very often differential equations don't have nice closed-form solutions, and I only expect to prove some qualitative stuff — mercio, Oct 03 '17 at 10:09
@mercio Well, I'm supposed to determine them and draw them. So I thought I should explicitly give these sets. — Siegfried Bernthaller, Oct 03 '17 at 10:13
though in your case those curves really look like level sets from some polynomial like (y² - kx²(x-a)) for some a and k — mercio, Oct 03 '17 at 10:35
wait a minute, the invariant function is in the title of your picture ? so you have already solved it ?? — mercio, Oct 03 '17 at 10:42
Do you know about first integrals of ODEs on planes? How integral curves and level sets of this first integral are related? Hamiltonian system is a particular example of system with first integral so this knowledge can be applied to it too. — Evgeny, Oct 03 '17 at 15:45
For this particular example see analysis in Miguel's answer. I've explained this stuff a bit in this answer. — Evgeny, Oct 03 '17 at 18:48

score 3 · Answer 1 · answered Oct 03 '17 at 18:30

Here are some ideas: The level sets

\[ \Gamma _{c} = \left\{ (x, x') : \frac{1}{2} (x')^2 - \frac{1}{2} x^2 + \frac{1}{3} x^3 = c \right\} \]

contain the orbits of the solution, because they provide a condition that $x (t), x (t')$ must fulfil for any valid $t$. Because orbits don't intersect, we know that $\Gamma_{0}$, which contains the constant solution $x \equiv 0$ for initial conditions $x = x' = 0$, is going to yield the critical value with which to investigate where $P, A_{-}, A_{+}, A$ lie.

You can play with the parameter $c$ with the desmos online grapher here.

For $c = 0$ you have orbits in one of three sets: the loop (not touching the origin) to the right is contained in a compact set so solutions will either be fixed points, periodic or approach the origin in infinite time (by Poincaré-Bendixson-ish). The two arcs to the left have this property in one direction in time, but not necessarily in the other (think of $x (t) = \frac{1}{t - t_{0}}$ for $t \downarrow t_{0}$).

For $c \in (c_{0} \ldots ., 0)$, with $c_{0} = 1/3 - 1/2$ (why?), orbits can be either enclosed in the little egg shape to the right or in the infinite arc to the left. Because the eggs are enclosed in a compact set (the oval), all initial conditions in the oval produce periodic solutions, i.e. they are in $P$.

You need to consider all cases and finish the arguments for each of them. Then you have statements about sets where $P, A_{-}, A_{+}, A$ are contained... which is a start :)

JJacquelin · Answer 2 · 2017-10-05T06:58:50.430

$$\begin{cases} \frac{dx}{dt}=y\\ \frac{dy}{dt}=x-x^2 \end{cases}\quad\to\quad \frac{dy}{dx}=\frac{x-x^2}{y}\quad\to\quad ydy=(x-x^2)dx$$ $\frac{y^2}{2}=\frac{x^2}{2}-\frac{x^3}{3}+$constant.

The equation of the orbit is : $$y(x)=\pm\sqrt{x^2-\frac{2}{3}x^3+C}$$ With initial point $(x_i,y_i)$ : $$C=y_i^2-x_i^2+\frac{2}{3}x_i^3$$

The shape of the trajectories depends on $C$ :

From $\quad\frac{dy}{dx}=\frac{x-x^2}{y}$ :

The trajectory is horizontal at $\left(x=0\:,\:y=\pm\sqrt{C}\right)$ and at $\left(x=1\:,\:y=\pm\sqrt{C+\frac{1}{3}}\right)$

The trajectory is vertical for $y=0$ and $x=$ roots of $x^2-\frac{2}{3}x^3+C=0$ .

So, we have to study the function $\quad C(x)=-x^2+\frac{2}{3}x^3$

I suppose that you can take it from here and show that $-\frac{1}{3}<C<0$.

The initial point $(x_i,y_i)$ must be in the range : $$-\frac{1}{3}<y_i^2-x_i^2+\frac{2}{3}x_i^3<0$$ Outside this range, the trajectories are going to infinity.

Note :

To answer to the question, there is no need to solve the equations for $x(t)$ and $y(t)$. This would involve a complicated analytical solving with elliptic integral on the kind $t(x)=\int \frac{dx}{\sqrt{x^2-\frac{2}{3}x^3+C}}$ .

In addition:

From $\quad\begin{cases} \frac{dx}{dt}=y\\ \frac{dy}{dt}=x-x^2 \end{cases}\quad$ a simple inspection allows to determine the direction of motion of the point $(x,y)$ when $t$ increases.

If $y>0$ , $x$ increases . If $y<0$ , $x$ decreases.

If $x<0$ , $y$ decreases . If $0<x<1$ , $y$ increases . If $x>1$ , $y$ decreases.

As already seen, if the initial point $(x_i\:,\:y_i)$ is in the range $\quad -\frac{1}{3}>y_i^2-x_i^2+\frac{2}{3}x_i^3\quad$ or in the range $\quad y_i^2-x_i^2+\frac{2}{3}x_i^3>0\quad$ there is no limit (black curves on the graph of trajectories).

$x'(t)$ and $y'(t)$ are more and more negative as $t\to\infty$. So, the point $(x,y)$ goes towards $(-\infty,-\infty)$ at increasing speed.

How can I separate which initial conditions only have limits to $t\rightarrow\infty$, those that only have $t\rightarrow-\infty$ and those that have both? — Siegfried Bernthaller, Oct 04 '17 at 18:13
In cannot understand your question. I added to my answer a description of the move of point $(x,y)$ as a function of $t$, depending on the range of the initial position. Hoping it help. — JJacquelin, Oct 05 '17 at 06:58

Periodic orbit of differential equation

2 Answers2