4

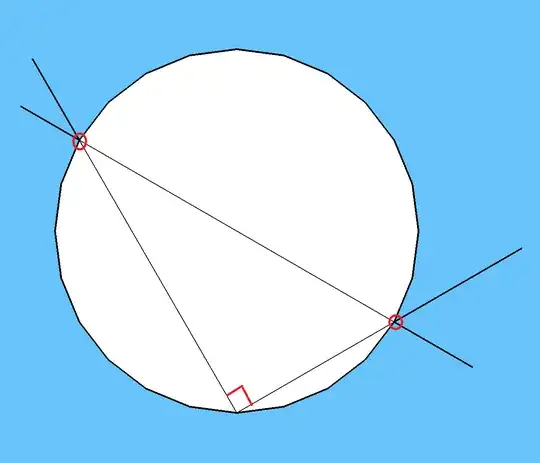
When I was 7 or 8 years old, I was playing with drawing circles. For some reason, I thought about taking a 90° angle and placing the vertex on the circle and marking where the two sides intersected the circle.

90° angle on a circle

It appeared to me that connecting the two points of intersection created a line through the center regardless of how the square was rotated.

90° angle on a circle with line connecting points of intersection

I tested this many times and, within the error my tools, my conjecture seemed to be correct. I had indeed discovered a method for finding the center of a circle. Simply create at least two of these bisecting lines and voila!

3 90° angles on a circle with lines connecting points of intersection that appear to meet in the center of the circle

The problem I have now, many years later, is that I am not satisfied with simply checking a bunch of times; I want a proof.

I can intuitively explain two extremes and the middle without any fancy math, but I still have not come up with a general proof.

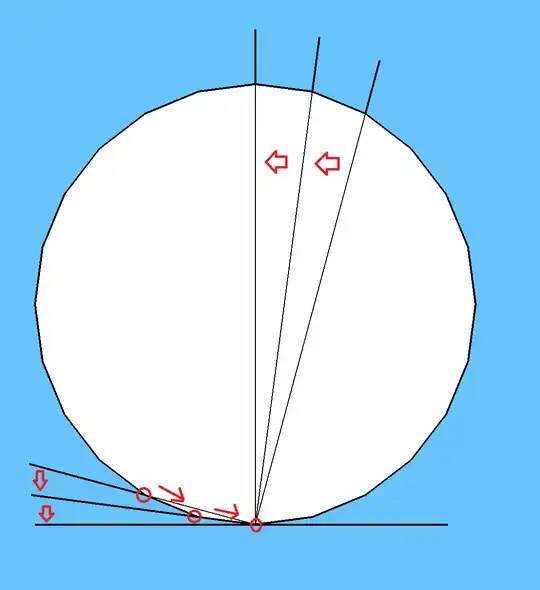
As one of the points of intersection approaches the vertex of the angle, the leg with that point approaches a tangent of the circle. It is intuitive to me that a line, which is perpendicular to a tangent line and passes through the point at which the tangent line touches the circle, would bisect the circle.

90° angle on a circle being rotated until one side is tangent to the circle

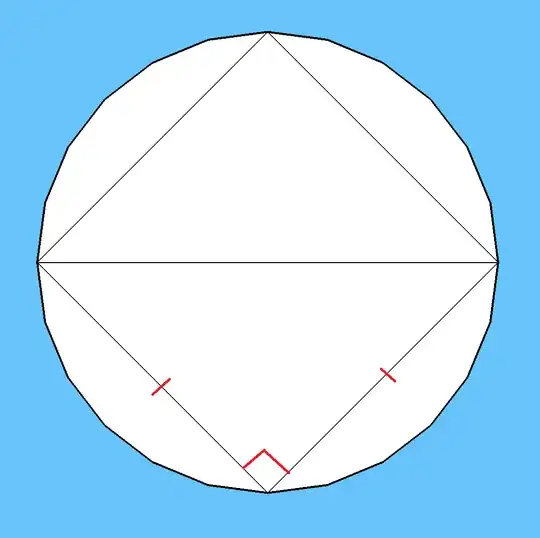
In addition, when the angle is rotated such that the two line segments formed between the vertex and the points of intersection are equal, these line segments form half of an inscribed square. A line that passes through two opposite vertices of that square would also bisect the circle.

Square inscribed in circle

Can you prove whether placing the vertex of a 90° angle on a circle creates a bisector by connecting the points of intersection?

Benjamin Cuningham
  • 143
  • 3
    First of all, I am very impressed by your insight and this question is presented very well. Keep it up. – Sarvesh Ravichandran Iyer Sep 02 '17 at 04:35
  • 2
    Nice(ly asked) question! One hint: look at inscribed angles. Another hint: the median of a right triangle drawn from the right-angle vertex equals half the hypotenuse, see for example here a proof without words. – dxiv Sep 02 '17 at 04:49
  • 1
    This is, specifically, (the converse of) Thales' Theorem. – Blue Sep 02 '17 at 05:07
  • 1
    @Blue Yes, I see. Thales' theorem is a special case of the inscribed angle theorem mentioned by dxiv . I can intuitively see that given the inscribed angle theorem, Thales' theorem must be true. My problem appears to be that this proof will mostly be a proof of the inscribed angle theorem, which I still do not quite understand. I will get there though. – Benjamin Cuningham Sep 02 '17 at 05:13

2 Answers2

1

This is (essentially) the converse of Thales' theorem:

The converse of Thales' theorem is then: the center of the circumcircle of a right triangle lies on its hypotenuse. (Equivalently, a right triangle's hypotenuse is a diameter of its circumcircle.)

The above quotation comes from the wikipage for Thales' Theorem, and the linked section contains three different proofs of this fact.

Benjamin Dickman
  • 16,038
1

Suppose that a triangle like the one in the picture has the median $AM$ equal to the half side $CB$ that is $CM=MB$.

You have an isosceles triangle $MCA$ with two equal angles and another, different, isosceles triangle $MBA$.

Now let's sum the angles $x+x+y+y=2x+2y=2(x+y)$ must give $180°$ which means that

$2(x+y)=180°$ that is $x+y=90°$.

Thus we have proved that if the midpoint of the longest side of a triangle has the same distance from the vertices the triangle is rectangle and we can draw a circle with centre $M$ and radius $MA$, the circumscribed circle.

enter image description here

Now let's assume that the triangle is rectangle and draw from the vertices of the longest side the parallels to the other shorter sides. They intersect at $D$ and is easy to see that $ABCD$ is a rectangle, whose diagonals are equal and cut each other in their midpoint. So it follows that $AM=BM=CM$.

We have proved that in a triangle rectangle the midpoint of the longest side has the same distance from the three vertex and is the centre of the circumscribed circle, that is the reason why when you where a child the right angles had sides which intersect the circle in points that are the diameter of the circle.

Hope this helps

enter image description here

Raffaele
  • 26,731