Intersection of triangle altitude feet with midpoint circle

Question

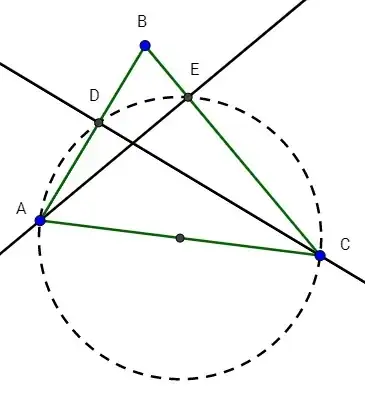
While playing around with this question, I seemed to find a relationship I wasn't aware of. A circle centered at the midpoint of a side of a triangle, and having that side as its diameter, intersects the feet of the altitudes from the endpoints of that side. See example below:

The circle centered at the midpoint of AC and having AC as its diameter, seems to intersect the feet E and D of the altitudes from points A and C.

I assume this is common knowledge, but couldn't immediately Google a proof. Can anyone show this is true?

It also follows from the property of right triangles that the length of the median drawn from the right-angle vertex is half the hypotenuse. See for example here a proof without words. — dxiv, Sep 02 '17 at 02:55

score 2 · Accepted Answer · answered Sep 01 '17 at 19:35

2

Hint: Use the fact that, if $XZ$ is a diameter of a circle, and $Y$ is a point on the circle, $\angle XYZ = 90^{\circ}$.

answered Sep 01 '17 at 19:35

Carl Schildkraut

37,483

score 0 · Answer 2 · answered Sep 02 '17 at 05:09

0

Think of it that way: Pick two arbitrary points D and E on the circumference. They will face the diameter on a 90 degree angle.. Expend AD and CE to create a triangle. Then, AE and CD are altitudes of the triangle...

answered Sep 02 '17 at 05:09

Panagos Papageorgiu

1

Intersection of triangle altitude feet with midpoint circle

2 Answers2