On the minimum eigenvalue of permutation matrices

Question

It can be shown that the maximum eigenvalue of a row-stochastic matrix is $1$, adapting, e.g. What are possible eigenvalues of a 0-1 (boolean) matrix?

A contrario no general result holds regarding its minimum eigenvalue. But, is it still true that no general result holds if one adds the condition that the matrix, in addition to being row-stochastic, is a permutation matrix ? Also, note that only their real parts is of importance to me.

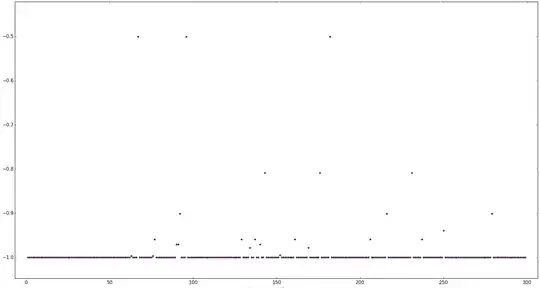
I did a simulation by randomly generating $300$ permutation matrices (incidentally, sometime not of full rank and that can be dimensionally reduced thus, not the point here). The chart of their Real parts follows.

None of their real part is lower than $-1$.

@Michael Burr Maybe a basis matrix is a permutation matrix ? Can you, Kanak, give some precision ? — Jean Marie, Aug 29 '17 at 12:32
Which means that ma question is likely to be a duplicate of, e.g. this one, isn't it ? Or at least to derive from it. — keepAlive, Aug 29 '17 at 12:38

score 2 · Accepted Answer · answered Aug 29 '17 at 12:46

Yes, the minimum eigenvalue is $-1$, but we can say more than that. The eigenvalues have to lie on the unit circle (and having an argument in $\pi\mathbb Q$)

The reason for this is that a permutation can be written as a product of disjoint cycles. In matrix terms this means that the matrix is a product of independent (cyclic) rotation matrices that has eigenvalues of $e^{2ik\pi/n}$.

On the minimum eigenvalue of permutation matrices

1 Answers1