I have been used SciLab for a day from now and I really excited to develop so called "H_{\infty}" controllers.
Normaly I have used LQG-controllers with integral actions, but I have heard that $H_{\infty}$ controllers is much better in real life because a $H_{\infty}$ controller do not require a perfect model of the system, as LQG-controller want to have.
If you look at this link: https://help.scilab.org/docs/6.0.0/en_US/section_64a8529216e858b335b0e6c058385350.html
You will find this:
- ccontrg — Central H-infinity continuous time controller
- dhinf — H_infinity design of discrete-time systems
- dhnorm — discrete H-infinity norm
- gamitg — H-infinity gamma iterations for continuous time systems
- h2norm — H2 norm of a continuous time proper dynamical system
- h_cl — closed loop matrix
- h_inf — Continuous time H-infinity (central) controller
- h_inf_st — static H_infinity problem
- h_norm — H-infinity norm
- hinf — H_infinity design of continuous-time systems
- linf — infinity norm
- linfn — infinity norm
- macglov — Continuous time dynamical systems Mac Farlane Glover problem
- nehari — Nehari approximant of continuous time dynamical systems
- parrot — Parrot's problem
My question is: What is important of this, if I want to develop a controller $K$ which have guaranteed stability margins - robustness.
I have two books about robust control, but I don't recognize anything when I read the list. What should I use? What should I focus on? The CACSD library for SciLab look like a mess.
Let's look at:
- h_inf - Continuous time H-infinity (central) controller
Ok! A $H_{\infty}$ controller!
Or should I use:
- ccontrg — Central H-infinity continuous time controller
My books tells me nothing about central controllers. So I guess that I have too start with the "ccontrg"....
Ok! The formula or code...what ever..tells me this:
[K]=ccontrg(P,r,gamma);
Ok! The $P$ is the agumented state space model, r..I don't know but gamma needs to be some kind of limit I guess?
The definition of $H_{\infty}$ is:
$$ ||F(P, K)||_{\infty} = max_{\omega}\bar{\sigma}(F(P, K)(i\omega))$$
Which means that our maximum singular value $E_{11}$(singular = positive value) of the
$$[U, E, V] = svd(P)$$
Cannot be larger that $\gamma$. So
$$max_{\omega}\bar{\sigma}(F(P, K)(i\omega)) < \gamma$$
Is the definition of $H_{\infty}$ controllers.
As you see...I know what I'm doing, but I still feel very unsure about this $H_{\infty}$ part of library. None of those functions asking the user about weighting matrices.
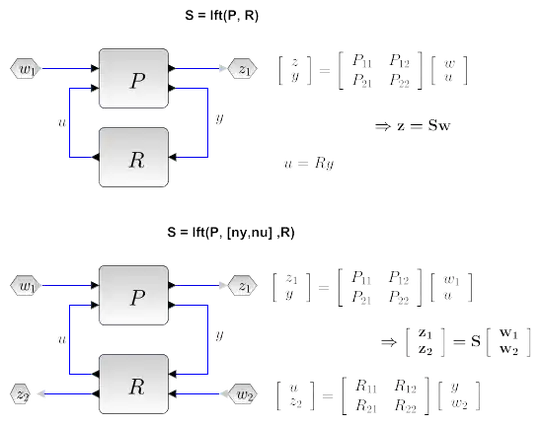
A $H_{\infty}$ controller look like the block diagram above. In this case $K = R$.