This question is rather a simple change of parameters in double integrals, that I am having problem understanding why is it correct.
Let $D=\left\{{(x,y)}, ~1\le x^2+y^2\le 4 ~ , x^2+y^2\le2x\right\}$, Find the area of $D$.
Now, the question is the same as saying find $\iint_D1dxdy$, considering polar representation $x=r\cos\theta, y=r\sin\theta, J=r$, it's the same as finding $\iint_{D'}rdrd\theta$
Now, the question is, why am I not summing to much area.
$D'=\left\{(r,\theta) | 1<r<2\cos\theta, \theta\in\frac{1}{3}[-\pi,\pi] \right\}$ according the solution.
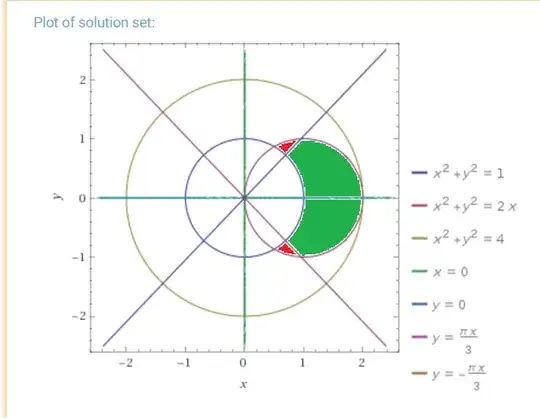
Now, it didn't make sense where the $\theta$ came from, so I plotted the area in wolframalpha.
Here is what the area looks like
Looking at the $D'$, it's calculating the arcs in the green, but not the red, the question is; where does the red goes?
I understand that manipulating the equation gets you the right formula, for example:
$1 \le x^2+y^2 \le 4 \Rightarrow 1 \le r^2 \le 4$
$x^2+y^2 \le 2x \Rightarrow r^2 \le 2r\cos\theta \Rightarrow r \le 2\cos\theta$
But then again, how do we find the $\theta$?