2

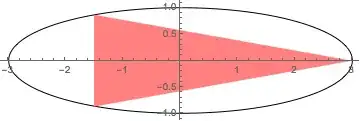
Find the maximum area of an isosceles triangle, which is inscribed inside an ellipse $\dfrac {x^2} {a^2} + \dfrac {y^2} {b^2} = 1$ with its (unique) vertex lying at one of the ends of the major axis of the ellipse.

The three vertices of the triangle would be $(a,0), (x,y), (x, -y)$.

The area of the triangle by Heron's formula is $$A^2 = (x-a)^2y^2 = (x-a)^2b^2\left( 1- \dfrac{x^2}{a^2}\right) \tag{1}.$$

Hence $$\dfrac{dA}{dx} = 0 \implies (x-a)^2 \left( x + \dfrac{a}2\right) = 0.$$

We have minimum at $x = a$ and maximum at $x = -\frac{a}{2}$.

Substituting back in $(1)$ and taking square roots on both the sides gives $$A = \dfrac{\sqrt{3}ab}{4}$$.

The given answer is $3A$.

What mistake I made ? Is it possible to find the answer to this question if the triangle was scalene ?

Michael Rozenberg
  • 203,855
user8277998
  • 2,856
  • How do you know the vertex on the major axis lies on the line of symmetry of the triangle? – Shuri2060 Aug 11 '17 at 20:42
  • @Shuri2060 Otherwise the triangle won't be isosceles. – user8277998 Aug 11 '17 at 20:46
  • Isosceles triangles can be inscribed without that condition. Take the triangle $(a,0),(-a,0),(0,b)$, for example. – Shuri2060 Aug 11 '17 at 20:48
  • The problem statement is that one vertex is at the end of a major axis. – David G. Stork Aug 11 '17 at 20:49
  • @DavidG.Stork The example I propose above isn't of the form $(a,0), (x,y), (x, -y)$ and has one vertex at the end of a major axis. There are examples where exactly one vertex is at the end of a major axis too. – Shuri2060 Aug 11 '17 at 20:50
  • @Shuri2060 Then in your case, it won't have its vertex at $(\pm a,0)$ which is the condition. – user8277998 Aug 11 '17 at 20:51
  • 1
    @123 If that is the case, then you (or the original problem) perhaps need to make it clear which vertex of the isosceles triangle is referred to. A triangle has three vertices. The example above has a vertex at one of those points. – Shuri2060 Aug 11 '17 at 20:53
  • @Shuri2060 You are correct, it is a vague statement but it is the original statement of the question. – user8277998 Aug 11 '17 at 20:54
  • @123 I'm not sure - but perhaps part of the problem is to also show that the maximum area is achieved when the major axis is a line of symmetry? (that may be false, in which case the original statement is indeed vague) – Shuri2060 Aug 11 '17 at 20:55
  • 1
    The problem states the triangle's [unique] "vertex" lies at $(a,0)$, so all is clear. – David G. Stork Aug 11 '17 at 20:59
  • @DavidG.Stork 'its vertex' does have an implication of uniqueness, but really, it isn't clear. – Shuri2060 Aug 11 '17 at 21:00

4 Answers4

2

By AM-GM $$S_{\Delta}=(a-x)y=(a-x)b\sqrt{1-\frac{x^2}{a^2}}=ab\left(1-\frac{x}{a}\right)\sqrt{1-\frac{x^2}{a^2}}=$$ $$=\frac{ab}{\sqrt3}\cdot\sqrt{\left(1-\frac{x}{a}\right)^3\left(3+\frac{3x}{a}\right)}\leq\frac{ab}{\sqrt3}\cdot\sqrt{\left(\frac{3\left(1-\frac{x}{a}\right)+3+\frac{3x}{a}}{4}\right)^4}=\frac{3\sqrt3ab}{4}.$$ The equality occurs for $1-\frac{x}{a}=3+\frac{3x}{a}$, which says that the equality indeed occurs,

which says that $\frac{3\sqrt3ab}{4}$ is a maximal value.

Done!

Michael Rozenberg
  • 203,855
  • Really cool method but I feel like this would be impossible to do without knowing the answer in the first place. – user8277998 Aug 12 '17 at 06:45
  • 2
    @123 I don't agree with you! We need just to delete $\frac{x}{a}$ inside the root and we made it by AM-GM. By the way, I did not know the answer before. – Michael Rozenberg Aug 12 '17 at 06:49
2

We perform an orthogonal projection to map the ellipse to the unit circle.

Let the maximal area of our isosceles triangle be $\mathcal{A}$ which we wish to find, and let $\triangle ABC$ be the isosceles triangle with maximal area inscribed in our unit circle. Since orthogonal projections preserve area ratios, $\triangle ABC$ is the projection of the triangle with area $\mathcal{A}$. Note that since we wish to maximise the area, $\triangle ABC$ is simply an equilateral triangle with area $\frac{3\sqrt{3}}{4}$. Hence, by preservation of area ratios,

$$\begin{align*} \frac{\mathcal{A}}{\text{ Area of ellipse}} &=\frac{[ABC]}{\text{ Area of circle}} \\ \implies \mathcal{A} &=\frac{3\sqrt{3}}{4\pi}\cdot \pi ab \\ &= \frac{3ab\sqrt{3}}{4} \end{align*}$$which is our answer.

user574848
  • 1,345
1

The given answer is correct. Your mistake is in the formula for the area, which should be $A/2 = 1/2\ {\rm base} \times {\rm height}$ for each half half triangle or

$A = (a-x) b \sqrt{1 - x^2/a^2}$

for the full triangle.

The derivative is then:

$${d A \over d x} = -\frac{b (a+2 x) \sqrt{1-\frac{x^2}{a^2}}}{a+x} .$$

Set it to $0$ to find $x = -a/2$.

Then compute the area:

$$A = {3 \sqrt{3} \over 4} a b$$

enter image description here

David G. Stork
  • 30,409
1

Everything is correct until you use the value of $x$ to calculate the area. You should have $$A^2=(-\frac{3a}{2})^2b^2(1-\frac 14)$$ which will give you the correct answer $$A=\frac{3\sqrt{3}}{4}ab$$

David Quinn
  • 35,087