Cover of "Gödel, Escher, Bach"

Question

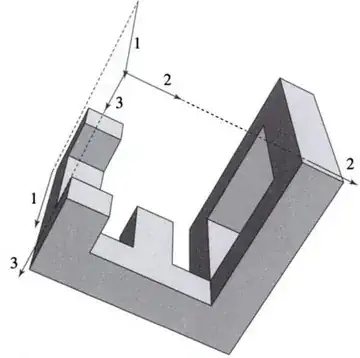
Consider the cover image of the book "Gödel, Escher, Bach", depicted below. The interesting feature is that it shows the existence of a subset of $\mathbb{R}^3$ which projects onto $\mathbb{R}^2$ in three different ways to form the letters of the book's title. It is natural to ask for generalizations: for which subsets $A_1, A_2, A_3$ of $\mathbb{R}^2$ is there set $X \subset \mathbb{R}^3$ such that, with $\pi_1, \pi_2, \pi_3$ the projection maps $\mathbb{R}^3 \rightarrow \mathbb{R}^2$, $\pi_1(X) = A_1, \pi_2(X) = A_2$, and $\pi_3(X) = A_3$?

More generally, let $\{ \pi_i \}_{i \in I_{n,m}}$ be the canonical projection maps $\mathbb{R}^n \rightarrow \mathbb{R}^m$, where $m \leq n$. For which sets $\{ A_i \}_{i \in I_{n, m}} \subset \mathbb{R}^m$ is there a set $X$ such that $\pi_i (X) = A_i \forall i \in I_{n, m}$?

Other interesting considerations:

1) I do not require the set to be connected. Nevertheless this presents an interesting question as to when the set in question is connected.

2) Let $X$ be the largest possible set satisfying the question, supposing it exists. Is there a simple way to calculate its boundary, $\partial X$?

3) What is the volume of the largest possible set in question in terms of $A_i$? It's worth noting that, if $A_1, A_2, A_3$ are measurable subsets of $I^2$, then there is an interesting formula for the volume of $X$ plus the volume of $Y = I^3 - \pi_1^{-1}(A_1) \cap I^3 - \pi_2^{-1}(A_2) \cap I^3 - \pi_3^{-1}(A_3) \cap I^3$.

Answer 1

The obvious (and maximal) candidate for the 3d object is $$\{\,(x,y,z)\in\Bbb R^3\mid (y,z)\in A_1, (x,z)\in A_2, (x,y)\in A_3\,\}$$ obtained by intersecting the maximal sets that give one of the three projections each. The question is if the projections of this maximal set are as desired. This is the case for the first projection if and only if for each $(y,z)\in A_1$ there exists $x\in\Bbb R$ such that $(x,y)\in A_3$ and $(x,z)\in A_2$. Similarly for the other two projections.

Hofstadter's examples work because already in the vertical bar of the E, there is so much material in the B (its lower line with final arc) that the G is guaranteed to work; and similarly, in the lower bar of the E, there is so much material in the G (its almost straight lower line) that the B is guaranteed to work; and finally the vertical bar of the B and the left end of the G are material enough to guarantee the E to work. So in a way, the trick is that the B and the G are less round than you might normally write them.

Answer 2

Ian Stewart, in one of the Scientific American columns, wrote on "What the hell is a digital sundial?" The idea was to define a shape that would cast a shadow showing the time as the sun moved across the sky. In a discussion of the Banach-Tarski paradox he essentially claimed that you could find a set to do any reasonable projections you want. I don't remember a careful proof being given. Wikipedia says the theorem was proved in 1987 by Kenneth Falconer.

Answer 3

This adds little to the discussion, but I made constructing an algorithm an exercise in Computational Geometry in C, p.154. It is a relatively easy program to write for orthogonal polygons, punching through the extrusion of each of the polygons orthogonally, and then checking whether or not the shadows are correct and the resulting 3D object is connected:

---

         

---

In fact, if you discretize the polygons to follow a grid, then the "punching through" can be achieved by traversing a 3D binary array.

Answer 4

Your generalization to triples $A_1, A_2, A_3$ for which there exists a single $X$ that projects to each of the $A_i$ is an example of the general phenomenon I have called $polysemy$. It's been explored in various applications in graph theory and order theory. A simple example question is, "For which pairs of partial orders $<_1$ and $<_2$ on a set $S$ does there exist a bijection $f:S\rightarrow{\mathbf R}^2$ such that for all $s,t \in S$, $$s <_1 t \iff d(f(s),\mathbf{0}) < d(f(t),\mathbf{0})$$ and $$s <_2 t \iff d(f(s),\mathbf{1}) < d(f(t),\mathbf{1}),$$ where $\mathbf{0}$ is the origin and $\mathbf{1}$ is the point (1,0)?"

For more info, see (of all places!) https://en.wikipedia.org/wiki/Representation_(mathematics)#Polysemy.

Answer 5

It seems to me like it is fairly simple to construct an object which generates almost any 3 projections you like. To make an example, consider only the closed unit cube in $\mathbb{R}^3$. Although not necessarily connected, the set $$\{(x,y,z)\in\mathbb{R}^3:(x,y)\in A_1||(z,y)\in A_2||(x,z)\in A_3\}$$ will generate $A_1$ along the z-axis, $A_2$ along the x-axis, and $A_3$ along the y-axis. For such a construction to be connected in $\mathbb{R}^3$, all three projections must be connected and when placed in the unit cube they all must containat least one of the four corners $(0,0),(0,1),(1,0),(1,1)$.

Essentially, take each projection and place them on the face of a rectangular prism as a 0-thickness subset of $\mathbb{R}^3$.

MORE METNIONED IN EDIT 3 STARTS HERE

We can actually do much better. We can account for the depth problem above by generalizing further.

This idea can be materialized. Let the orthogonal axes in question be defined by unit vectors $\vec{a_1}$, $\vec{a_2}$, and $\vec{a_3}$. The following will all work when projections $A_1$ through $A_3$ are connected.

We define $A_n'$ as the extension of $A_n$ into $\mathbb{R}^3$ as a prism. More formally, $$A_n'=\{(b_1,b_2,b_3)|\sum_{1\le i\le 3, i\not=n}{b_i\vec{a_i}}\in A_n\}$$ Then the set with largest volume that generates the 3 projections (without considering rotation) is $X=A_1'\cap A_2'\cap A_3'$.

EDIT: as pointed out in the comments, It is not necessary for the projections to contain a corner to be connected, but if they contain the corner and are connected themselves they will be connected.

EDIT 2: To clarify, I mean almost any triplet of projections vaguely because I have been unable to form the idea further. This is only a construction that covers "nice" projections, and is kind of a cookie cutter idea. It's intuitively based on just attaching the projections to the face of a cube; this would generate each projection on the face it's placed, plus any edge from the other (which can be fixed often by changing the depth of the other projections) but this is where I've had trouble formalizing anything. I have a log flight upcoming, hopefully I can develop this further there.

EDIT 3: Added some more (above edits).