Differentiability of the sum of $\sum_{n=1}^{\infty}\frac{\sin(nx)}{n^2}$

Question

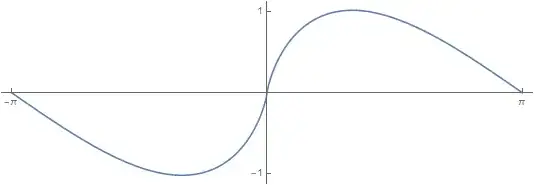
Consider the series $$\sum_{n=1}^{\infty}\frac{\sin(nx)}{n^2}$$ This series converges uniformly to a continuous function, by Weierstrass's test, and it is the Fourier series of its sum, I'll call $f(x)$.

Is $f$ continuously differentiable in $[-\pi, \pi]$?

The common criterion to determine differentiability of the sum of uniformly convergent series is by testing uniform convergence of the series of derivatives. But I don't see how it's applicable here.

This question: The Fourier series $\sum_{n=1}^\infty (1/n)\cos nx$ calculates the sum of the derivatives.

But is there an argument to say that $f$ is not differentiable (based on the answer there), without calculating the explicit sum?

Answer 1

We can see that $f$ isn't differentiable at $0$ [and generally at $2m\pi$ by periodicity] by estimating the difference quotient

$$\frac{f(x_k) - f(0)}{x_k}$$

for a suitable sequence $(x_k)$ converging to $0$. Let's choose $x_k = \frac{1}{k}$. Then we have

$$f(x_k) \geqslant \sum_{n = 1}^k \frac{1}{n^2}\sin \frac{n}{k} - \sum_{n = k+1}^{\infty} \frac{1}{n^2} > \frac{2}{\pi k} \sum_{n = 1}^k \frac{1}{n} - \frac{1}{k} > \biggl(\frac{2}{\pi}\log k - 1\biggr)x_k$$

since $\sin x > \frac{2}{\pi} x$ for $0 < x < \pi/2$, $\sum_{n = 1}^k \frac{1}{n} > \log k$, and $\sum_{n = k+1}^{\infty} \frac{1}{n^2} < \sum_{n = k+1}^{\infty} \frac{1}{n(n-1)} = \frac{1}{k}$. So we directly see that

$$\lim_{k\to\infty} \frac{f(x_k)}{x_k} = +\infty.$$

Answer 2

By the Dirichlet's test, the series $\sum_{n=1}^{\infty} \frac{\cos(nx)}{n}$ converges uniformly on $[-\pi,\pi]\setminus(-\delta,\delta)$ for every $\delta > 0$. So it follows that $f$ is differentiable on $[-\pi,\pi]\setminus\{0\}$ and its derivative is given by the term-wise differentiation

$$ f'(x) = \sum_{n=1}^{\infty} \frac{\cos (nx)}{n}, \qquad x \in [- \pi,\pi]\setminus\{0\}. $$

At $x = 0$, @Daniel Fischer's answer shows that $f'(0)$ does not exist. In fact, accompanied by the actual computation $f'(x) = -\frac{1}{2}\log(2 - 2\cos x)$ for $x \neq 0$ and by mean value theorem, we can prove that $f'(0) = +\infty$.

$\hspace{3em}$