Let $l$ be a line not intersecting circle $\omega$ that has center $O$. Draw $OP$ perpendicular to $l$ at point $P$ and draw $PA$ tangent to $\omega$ at point $A$. Extend $OA$ to cut $\omega$ again at point $B$ and cut $l$ at point $C$. $PB$ cuts $\omega$ at point $D$ and $AD$ cuts $l$ at point $E$. Prove that $PE=PC$.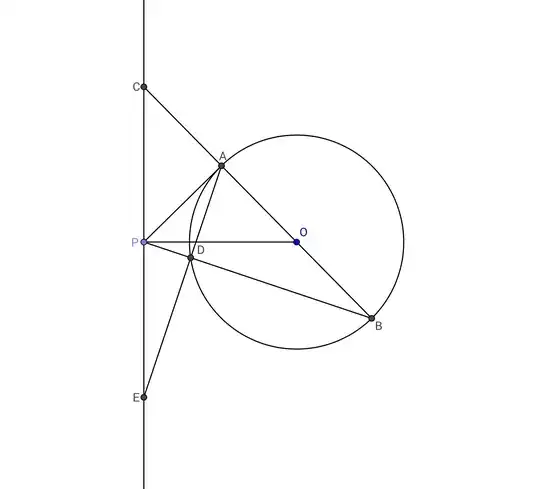
My thought :
Pole of point $P$ passes point $A$.
Since $P, C, E$ are collinear, so polar of $P, C, E$ are concurrent.
From the Menelaus Theorem on $\triangle CBP$ and the line $A-D-E$ we have:
$$\frac{CA}{AB} \times \frac{BD}{DP} \times \frac{PE}{CE} = 1$$
So from this it's enough to prove that $\frac{CA}{AB} \times \frac{BD}{DP} = 2$.
Now we have that $AB = 2R$, while from the power of point $P$ we get: $DP = \frac{PA^2}{PB}$. Using some well-known formulas for altitudes in right-angled triangles we have:
$$\frac{CA}{AB} \times \frac{BD}{DP} = \frac{CA \cdot BD \cdot PB}{2R \cdot AP^2} = \frac{BD \cdot PB}{2R^2} = \frac{AB^2}{2R^2} = \frac{4R^2}{2R^2} = 2$$
Hence the proof.
Let $OA=r$ and $\measuredangle POA=\alpha$.
Hence, $PA=r\tan\alpha$ and since $AB=2r$, we get $$\sin\measuredangle PAE=\sin\measuredangle B=\frac{\tan\alpha}{\sqrt{\tan^2\alpha+4}}.$$ Now, since $\measuredangle CPA=\alpha$, we obtain $$\sin\measuredangle E=\sin\left(\alpha-\arcsin\frac{\tan\alpha}{\sqrt{\tan^2\alpha+4}}\right)=$$ $$=\sin\alpha\cdot\sqrt{1-\frac{\tan^2\alpha}{\tan^2\alpha+4}}-\cos\alpha\cdot\frac{\tan\alpha}{\sqrt{\tan^2\alpha+4}}=\frac{\sin\alpha}{\sqrt{\tan^2\alpha+4}}.$$ Thus, by law of sines for $\Delta PAE$ we obtain $$\frac{PE}{\frac{\tan\alpha}{\sqrt{\tan^2\alpha+4}}}=\frac{r\tan\alpha}{\frac{\sin\alpha}{\sqrt{\tan^2\alpha+4}}},$$ which gives $$PE=\frac{r\sin\alpha}{\cos^2\alpha}.$$ In another hand, $$CP=\frac{AP}{\cos\alpha}=\frac{r\tan\alpha}{\cos\alpha}=\frac{r\sin\alpha}{\cos^2\alpha}$$ and we are done!
Observe that $ \angle \, EDP = \angle \, ADB =90^{\circ}$ and $ \angle \, EPO =90^{\circ}$ therefore $$\angle \, AEP = \angle \, BPO \,\, \text{ and } \,\, \angle \, APE = \angle \, BOP$$ the latter identity following from the fact that triangle $CPO$ is right angled with right angle at vertex $P$ and the fact that $PA$ is perpendicular to $CO$ because $PA$ is tangent to the circle and $OA$ is a radius. Thus triangles $AEP$ and $BPO$ are similar so $$\frac{AP}{EP} = \frac{BO}{PO} = \frac{AO}{PO}$$ However the right angled triangles $APO$ and $ACP$ are similar, so $$\frac{AO}{PO} = \frac{AP}{CP}$$ leading to the identity $$\frac{AP}{EP} = \frac{AO}{PO} = \frac{AP}{CP}$$ i.e. $$\frac{AP}{EP} = \frac{AP}{CP}$$ which after cross-multiplying yields $$AP \cdot CP = AP \cdot EP$$ i.e. $$CP = EP$$
Set coordinate system at $O(0,0)$ and $PO$ ay $x$-axis. Let $r=1$ and let $y=kx$ be line $AB$. Then $A(a,ak)$ and $B(-a,-ak)$ for some $a$. Thus $a^2(1+k^2)=1$.
Perpendicular at $A$ to $AB$ is line $y-ka = -{1\over k}(x-a)$ which cuts $x$-axis at $P({1\over a},0)$. So $CE$ is perpendicular to $x$-axis through $P$. Line $AB$ cuts $PE$ at $C({1\over a},{k\over a})$.
Perpendicular to $BP$ through $A$ $$ y- ka = {1+a^2\over ka^2}(x-a)$$
cuts $PC$ at $E$: $x_E= {1\over a}$ and $$y_E = ka-{1+a^2\over ka^2} ({1\over a}-a) = ... =-y_C$$
Here is another, projective solution.
Let $p$ be polar for $P$ and let it cuts $BD$ at $A'$. Clearly $p$ must go through $A$ since $P$ is on tangent for $A$ which is polar for $A$. Since $p\bot PO$ we have $EC||p$, thus $EC \cap p = \infty$. Now: \begin{eqnarray*} (E,C;P, \infty) &= &(AE, AC;AP, A\infty) \\ &=& (AD,AB;AP,AA') \\ &=& (D,B;P,A') =-1 \end{eqnarray*} and thus $C$ halves a segment $EC$.