An odd (potential) primality test

Question

My friend and I were talking about primality testing, and he showed me a really neat way to test if something is prime or not. The thing is, we have no idea how it works.

So, we want to test if $n$ is prime. Draw an $n$-gon. Start at any vertex, and draw a line from that point to the adjacent vertex (this can be any direction as long as it's consistent through the whole process). Then go from that vertex, and go over two vertices. Start there and go over 3 vertices, etc. until the pattern repeats itself. For example, if $n$ is $5$ we draw a pentagon:

       • (a)

 • (e)       • (b)


  • (d)     • (c)

And A->B, then B->D, then, D->B, then B->A, and finally A->A (you don't have to draw anything). The sequence then repeats itself infinitely so we stop there. What we've found is that for any $n$-gon where $n$ is prime (and only when $n$ is prime), no vertices have more than one line drawn to them. Intuitively I have some idea of why this means it's prime, but I can't exactly grasp it.

Pictures:

Why does this work? Does it even work past a certain number? What's the mathematical principle behind it, and can we represent this test mathematically without drawing shapes?

Answer 1

Note: this is not a complete solution, but rather, a not-too-beautifully constructed proof of half the claim ("If you get multiple hits, then $n$ isn't prime"), with a brief discussion of why the other half might be true, but why it's a bit marginal, and leaves me doubting that it works.

The vertices you hit (assuming the starting vertex is labelled $0$ are of the form $$ 1\\ 1 + 2\\ 1 + 2 + 3 \\ \ldots $$ all $\bmod n$, where $n$ is the number you're testing for primality. These can be rewritten in the form $1 + 2 + \ldots + k = \frac{k(k+1)}{2}$, so you're getting vertices $$ 1\\ \frac{1(2)}{2} \\ \frac{2(3)}{2} \\ \frac{3(4)}{2} \\ \frac{4(5)}{2} \\ \ldots $$

(again, all $\bmod n$). Suppose that two of these are equal, i.e., that $$ \frac{u(u+1)}{2} = \frac{v(v+1)}{2} \bmod n $$

Then $$ u^2 + u - v^2 - v = 0 \bmod n $$ and thus $$ (u+v)(u-v) + (u-v) = 0 \bmod n $$ and hence $$ (u+v+1)(u-v) = 0 \bmod n $$ Now since $u$ and $v$ are distinct, that means that $u-v$ divides $n$, and (if it's not $1$) that $n$ is not prime.

So I guess that shows that if you get a repeat, then $n$ is not prime.

What's not clear is that if $n$ is not prime, then you must get repeats, for if your polygon comes back to vertex $0$ after some numbers of steps less than, say, $\sqrt{n}$, then there might be a factor that you "never get a chance to see." On the other hand, in $\sqrt{n}$ steps, you only get a sum that's $\sqrt{n} (\sqrt{n} + 1)$ in size, i.e., $n + \sqrt{n}$. So this is right on the margin.

It's POSSIBLE that the loop closes up in just under $\sqrt{n}$ steps, but that $n$ itself happens to be the square of a prime. You'd have to prove that can't happen before I'd believe the "only if" part of the claim.

(And hence, as @Bram28 / @Nilknarf observe, you don't have a primality checker until you do this "marginal" part.)

Answer 2

I'll collect my comments into one answer that amends the ones by John Hughes and Doug M. The upshot is: The "test" sorts out primes and powers of 2.

As both other answers noted, more than one edge hitting two edges touching a vertex in the "test" is equivalent to: There are $0 \le v \neq u \le n-1$ such that

$S_v \equiv S_u$ mod $n$,

where $S_i := \sum_{j=0}^i i= \displaystyle\frac{i(i+1)}{2}$.

Edit: It is a bit more complicated: $S_u$ being the number of a vertex means there are up to two edges touching it, one of length $u$ and one of length $u+1$. Since wlog $n>1$, in case $u\neq 0$ there are exactly two, and if $u=0$, interchange $u$ and $v$ to see that the following consideration also takes care of that case. There is one possibility (beside $u=v$) where $S_u \equiv S_v$ mod $n$ is allowed, because no extra edges appear in the graph: Namely, when $u \equiv -v-1$ mod $n$, or equivalently with our inequalities, $u+v+1=n$. Because then the edge after $v$ steps ("going in to $S_v \equiv S_u$") is the one of the $u+1$-step "drawn backwards", and the next is the one of the $u$-th step "drawn backwards". Actually, this does happen for all odd $n$, prime or not. So "Passing the test" i.e. not more than two edges touching each vertex translates to "If $S_u \equiv S_v$ mod $n$, then either $u=v$ or $u+v+1=n$". This does not change the outcome of the following though.

Notice that after $n$ steps, there is periodicity because, for $0 \le k\le n-1$, (as Doug M notes) $S_{n+k} \equiv S_{n-k-1}$ mod $n$, and more generally but with basically the same calculation $S_{rn+k} \equiv S_{rn-k-1}$ mod $n$. Graphically this means that always you eventually move back and forth in the graph that appeared after your first $n-1$ steps.

Proposition: A number $n$ passes the test (i.e. no "multiple hit" appears in the graph) if and only if $n$ is either a prime or a power of $2$. (So primes and 4,8,16,32 ... pass the test, but no other numbers.)

Proof: First notice that if $u-v=1$ then $S_u-S_v=u \not\equiv 0$ mod $n$, so the case $u-v=1$ cannot occur.

To see that prime $n$ pass the test, see both quoted answers (plus that observation).

Edit ... and note that the only possibility left is $u+v+1=n$, which, as said, still passes the test.

To see that $n=2^k$, $k\ge 2$, passes the test, assume we had $u,v$ as above. Then like in John Hughes' answer it follows that $(u+v+1)(u−v)=0$ mod $n=2^{k}$, and because we know $u-v \neq 1$ but also $u-v <2^k$ by our assumed inequalities, the factor $u-v$ contains a power of 2 greater than 1 and less than $k$, so the other factor $u+v+1$ must contain some power of 2. But then both factors would have to be even, which cannot be: If $u-v$ is even, $u$ and $v$ have the same parity which makes $u+v+1$ odd.

Now the converse, i.e. all other numbers fail the test:

First (easier) case, $n$ is an odd composite number. Observe that then $2$ is invertible mod $n$. Write $n=a\cdot b$ with $1<a,b<n$. Choose any representatives of $u=(a+b−1)/2$, $v=(a−b−1)/2$ mod $n$ (observe that $u-v \equiv b$ mod $n$): They will do the trick, as the computation in John Hughes' answer is completely reversible modulo $n$, including the division by 2.

Edit: Also, $u+v+1 \equiv a \not\equiv n$ mod $n$.

Example: $n=15=3\cdot 5$. The inverse of 2 modulo 15 is 8, so we can set $u=(3+5-1)\cdot 8 \equiv 11$ mod $15$ and $v=(3-5-1)\cdot 8=-24 \equiv 6$ mod $15$, and you can check that the same vertex is hit "from different directions" at step 6 and 11. (Or, $S_6=21 \equiv S_{11}=66 \equiv 6$ mod $15$.)

Other example: $n=21 = 3\cdot 7$. The inverse of 2 modulo 21 is 11, so we set $u=(3+7-1)\cdot 11 \equiv 15$ mod $21$ and $v=(3-7-1)\cdot 11 \equiv 8$ mod $21$. If you went on in your picture, you would see that the vertex at step 8 is hit again from different directions at step 15. (I'm not claiming the method finds every multiple hit, and there is already one at steps 5 and 8 as you note.)

Second case, $n$ is even but not a power of $2$. So $n=2^k m$ with $k\ge 1$ and $m >1$ odd.

We have to be careful about powers of 2 and getting $u$ and $v$ between $0$ and $n-1$ now, because the formula $\frac{u(u+1)}{2}$ is not well defined for $u \in \mathbb{Z}/n$.

• If $2^{k+1}-m-1 \ge 0$, we can set $u=\frac{1}{2}(2^{k+1}+m−1)$ and $v=\frac{1}{2}(2^{k+1}−m−1)$. One checks that $u$ and $v$ lie between $0$ and $n-1$ (here, $u\le n-1$ is maybe the hardest to show, but doable). A little computation with the binomial theorem and keeping track of the right powers of 2 shows that $\frac{u(u+1)}{2}=\frac{v(v+1)}2$ mod $n$. Further, it's easily seen that $u-v \equiv m \not\equiv 0$ mod $n$.

  Edit: And $u+v+1=2^{k+1} \neq n$.

  So we have a true, visible double hit with at least four distinct edges touching the vertex.

  Example: $n=20= 2^2\cdot5$ gives $u=6$, $v=1$ which is a double hit in your picture, although you did not mark it red.

• If $2^{k+1}-m-1 < 0$, choose $r >1$ minimal such that $2^{k+r}-m-1 \ge 0$. (In other words, $m+1 \le 2^{k+r}\le 2m+2$). Then set $u=\frac{1}{2}(2^{k+r}+m−1)$ and $v=\frac{1}{2}(2^{k+r}−m−1)$. Basically the same computation as before shows $\frac{u(u+1)}{2}=\frac{v(v+1)}2$ mod $n$. Again $u-v \equiv m \not\equiv 0$ mod $n$, and the inequalities make sure (... skip little nasty computations ...) that $u$ and $v$ lie between $0$ and $n-1$.

  Edit: As well as $u+v+1=2^{k+r} \neq n$.

  Example: $n=26 =2\cdot 13$ gives $r=3$, $u=14$ and $v=1$. Check for yourself that in a 26-gon, the same vertex is hit after 1 and 14 steps. (Or observe that $105=S_{14} \equiv 1=S_1$ mod 26, it is the first vertex touched by an edge of length 1 ("going in"), one of length 2("going out"), one of length 14 ("going in") and one of length 15 ("going out"). Maybe there are even more.)

Answer 3

If we number the vertices from $0$ to $p-1$ and start at vertex $0$

Then we can describe the circuit as $S_n = \sum_\limits {i=1}^n i \pmod p$

If $p$ is prime, then each vertex is attached to no more than $2$ lines.

However, this is not an "if and only if" proposition. i.e. it fails when $p=4$ and not a "prime checker"

Proving it the one way...

If $p = 2$ the graph is trivial.

if $p$ is odd, when we reach $k=\frac {p-1}{2}$

$S_{k+1} = S_{k-1}$

i.e. $S_k + \frac {p+1}{2} \equiv S_k + \frac {p+1}{2} - p \equiv S_k - \frac {p-1}{2} \pmod p$

and it is easy enough to show that $S_n = S_{p-n-1}$ and the circuit doubles back on itself.

We need to show for all $m,n: 0\le n,m \le \frac {p-1}{2}, S_n-S_m \ne 0$ and $m\ne n$

$S_n-S_m \equiv 0\pmod p$

$S_n-S_m = \frac 12 (n-m)(n+m+1)$

And with $p$ prime, there is impossible for two numbers smaller than $p$ to have a product that is a multiple of $p$

Answer 4

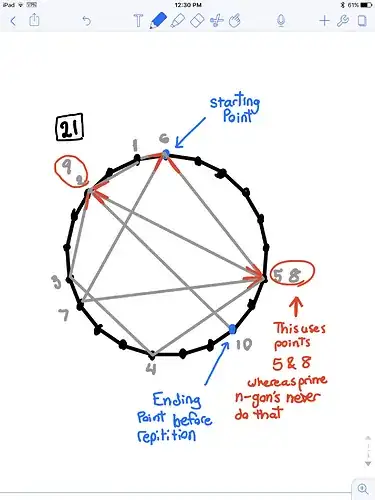
I would like to add this explanation as a complement to the rest of answers. I think that the problem can be stated as a rotation problem of $D_n$, the Dihedral group of the $n$-gon. This is only the statement and an explanation of the equivalence.

When you trace a line from vertex $v_i$ to vertex $v_j$, imagine that you are not joining them with a line, but rotating to the right the $n$-gon, $k$ times $\frac{360}{n}$ degrees (the angle between two consecutive vertices) where $k$ is the total of rotations of one vertex $v_i$ to the closest vertex $v_{i+1}$, in the decided rotating direction to the desired final $v_j$ that you need to arrive at $v_j$ from $v_i$.

The Caley table of the Dihedral group of the $n$-gon, $D_n$, shows the composition operation between the elements of $D_n$. The composition operation of rotations basically is defined as $$r_ir_j=r_{i+j \pmod {n}}$$

... where $i,j \in [0..n-1]$. The operation is right to left: we apply rotation $r_i$ to the already made rotation $r_j$. The composition operation is the group operation of $D_n$.

Supposing that $I=r_0$ is the initial position of the $n$-gon at the beginning of the conjecture, then you rotate $r_1$ times the angle between two consecutive vertices (this is rotating $\frac{360}{n} \cdot 1$ degrees to the right), then you rotate $r_2$ times ($\frac{360}{n} \cdot 2$ degrees to the right), then three times, etc.

The "jumps", or lines traced between vertices, are equivalent to rotations. Jumping $20$ vertices will be equivalent to applying the $n$-Dihedral group rotation $r_{20 \pmod {n}}$.

So basically $r_{i+1 \pmod {n}}r_{i \pmod {n}} = r_{i+1+i \pmod {n}} =r_{2i+1 \pmod {n}}$. So it is equivalent to make operations in the rotations of the Caley table of $D_n$.

This is an example of $D_5$

$$\begin{array}{|c|c|c|c|c|c|} \hline & r_0& r_1 & r_2 & r_3 & r_4 \\ \hline r_0 & \color{red}{r_0} & \color{red}{r_1} & r_2 & r_3 & r_4 \\ \hline r_1 & r_1 & r_2 & \color{red}{r_3} & r_4 & \color{red}{r_0} \\ \hline r_2 & r_2 & r_3 & r_4 & r_0 & r_1 \\ \hline r_3 & r_3 & r_4 & r_0 & \color{red}{r_1} & r_2 \\ \hline r_4 & r_4 & r_0 & r_1 & r_2 & r_3 \\ \hline \end{array}$$

As per your conjecture, we start at $r_0$ (column). We will mark in red $r_0$ because we will assume that the first movement of the conjecture is rotate $0$ degrees, so $r_0r_0=r_0$. Then we apply to the current rotation type, that happens to be again $r_0$, a rotation $r_1$, so we are at $r_1$, now again going to the column $r_1$ now we will apply a rotation of $r_2$, so $r_2r_1=r_3$, so we will mark $r_3$ in red... if we continue the algorithm, we will arrive to a Caley table in which every column has only one visited rotation type.

If we find two rows with the same rotation type marked in red, means that a vertex has more than two lines entering or exiting it.

But, as the other answer said, also holds for $D_{2^t}$ cases, for instance $D_4$

$$\begin{array}{|c|c|c|c|c|} \hline & r_0& r_1 & r_2 & r_3 \\ \hline r_0 & \color{red}{r_0} & \color{red}{r_1} & r_2 & r_3 \\ \hline r_1 & r_1 & r_2 & \color{red}{r_3} & r_0 \\ \hline r_2 & r_2 & r_3 & r_0 & r_1 \\ \hline r_3 & r_3 & r_0 & r_1 & \color{red}{r_2} \\ \hline \end{array}$$

And apart from those cases, we will find two red marks $\color{red}{r_3}$ with the same rotation type, for $D_{6}$:

$$\begin{array}{|c|c|c|c|c|c|c|} \hline & r_0& r_1 & r_2 & r_3 & r_4 & r_5 \\ \hline r_0 & \color{red}{r_0} & \color{red}{r_1} & r_2 & r_3 & \color{red}{r_4} & r_5 \\ \hline r_1 & r_1 & r_2 & \color{red}{r_3} & r_4 & r_5 & r_0 \\ \hline r_2 & r_2 & r_3 & r_4 & r_5 & r_0 & r_1 \\ \hline r_3 & r_3 & r_4 & r_5 & \color{red}{r_0} & r_1 & r_2 \\ \hline r_4 & r_4 & r_5 & r_0 & r_1 & r_2 & \color{red}{r_3} \\ \hline r_5 & r_5 & r_0 & r_1 & r_2 & r_3 & r_4 \\ \hline \end{array}$$

If we use the Caley table to perform the same original algorithm that the OP defined, then our stop condition is arriving to a rotation of $n-1$ vertices successfully or marking for the second time in red the same rotation type (as in the former case happened with $r_3$).

So basically if my expressions above are correct, your conjecture (including the observation that also the set $2^t$ holds) can be stated as:

$\forall D_n\ ${$\not \exists r_a,r_b,r_c,r_d,r_e \in D_n, a \not = b \ ,\ r_c r_a=r_e \land r_dr_b=r_e $}$ \to n \in \Bbb P\ \cup\ ${$2^t,t \in \Bbb N, t \ge 2$} where $D_n$ is the Dihedral group of the $n$-gon.

or equivalently:

Def. Set $E_n = ${$e_k: e_k=r_k r_{k-1}...r_0, k \in \Bbb N, k \lt n $}

$\forall D_n\ ${$\not \exists e_i,e_j,i \not = j \in E_n: e_i=e_j $}$ \to n \in \Bbb P\ \cup\ ${$2^t,t \in \Bbb N, t \ge 2$}

That would be the initial point for a demonstration. I am currently reading the book "Symmetry: A Mathematical Exploration (Springer, Kristopher Tapp)" and this conjecture fits very well with the basic concepts explained about the Dihedral group in the book. Is a good reading for beginners (like myself).